7. Вращение плоскости колебаний. Что такое удельное вращение и от каких факторов оно зависит?
8. Принцип действия простейшего поляриметра, состоявшего из поляризатора, анализатора и оптически активного раствора. Почему подобный поляриметр не находит применение в практике?
9. Объясните, пользуясь векторной диаграммой, прохождение света через поляриметр Корну.
10.Устройство и принцип действия поляриметра СМ.
11.Почему при работе с полутеневыми поляриметрами рекомендуется пользоваться монохроматическим светом?
Литература:
1. Ландсберг Г.С. Оптика.- М: Наука, 1976.
2. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике.- М: Высшая школа, 1965.
3. Корсунский М.И. Оптика. строение атома, атомное ядро. – М.; Наука, 1967.
ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА ОТ УЗКОЙ ЩЕЛИ
Цель работы – получить дифракционную картину от щели, определить ширину щели, изучить распределение интенсивности в дифракционной картине.
Приборы и принадлежности: гелий-неоновый лазер, гальванометрический усилитель, электронный автоматический потенциометр, экран для наблюдения дифракционной картины, самописец, фотодиод.
Теоретическое введение
Дифракцией света называется отклонение света от прямолинейного распространения, когда свет, огибая препятствие, попадает в область геометрической тени. В результате дифракции происходит перераспределение световой энергии в пространстве, и возникает система чередующихся светлых и темных полос – дифракционная картина.
Если на пути световой волны поместить непрозрачный диск (рис. 1), то при определенных условиях на экране возникает дифракционная картина, в центре которой наблюдается светлое пятно.

Рис.1. Дифракция на диске. РИСУНОК НЕ ЗАВЕРШЕН?!
Наиболее отчетливо явление дифракции наблюдается, когда размеры препятствия D удовлетворяют условию
D £ ![]() , (1)
, (1)
где l – расстояние от точки наблюдения до
препятствия; l
– длина волны. При сравнительно большом D, т.е. когда ![]() << D , волновые эффекты незаметны, и можно говорить о
выполнении законов геометрической оптики.
<< D , волновые эффекты незаметны, и можно говорить о
выполнении законов геометрической оптики.
Явление дифракции можно объяснить с помощью принципа Гюйгенса, согласно которому каждая точка волнового фронта является источником вторичных сферических волн, огибающая которых дает положение фронта волны в следующий момент времени. На рис. 2 показана плоская волна, падающая на щель. В соответствии с принципом Гюйгенса каждая точка участка волнового фронта становится источником вторичных волн.
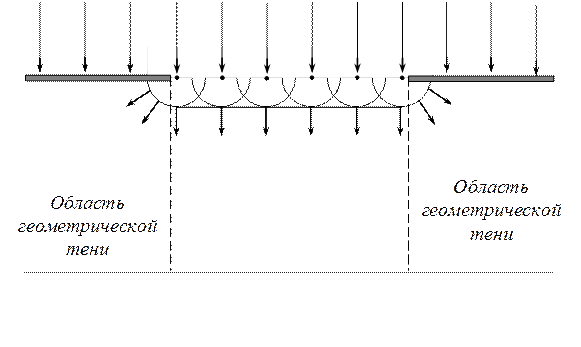
Рис.2. Схема дифракции на щели по принципу Гюйгенса
Вторичные источники испускают свет по всем направлениям, и световые волны могут попадать в любую точку экрана, в том числе и в область геометрической тени (рис. 2).
Принцип Гюйгенса объясняет явление дифракции качественно, но не позволяет найти распределение интенсивности света в дифракционной картине. Френель устранил этот недостаток, дополнив принцип Гюйгенса принципом интерференции вторичных волн. Согласно Френелю, световой эффект в любой точке пространства можно рассматривать как результат интерференции вторичных волн, поступающих в данную точку от всех элементов, на которые разбивается волновой фронт.
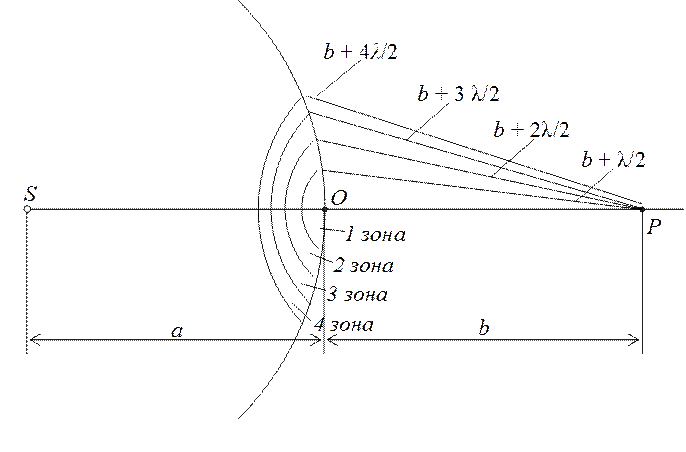
Рис. 3. Схема разбиения фронта сферической волны на зоны Френеля.
Для случаев, отличающих симметричной формой фронта волны, Френель предложил удобный и наглядный метод нахождения амплитуды результирующего колебания – метод зон Френеля. Согласно этому методу, волновой фронт разбивается на такие участки (зоны Френеля), расстояние от которых до точки наблюдения изменяется от зоны к зоне на l/2 (рис. 3). При таком разбиении световые волны, приходящие в точку наблюдения P от двух соседних зон, окажутся в противофазе и будут гасить друг друга.
Пусть свет падает на препятствие с отверстием или со щелью. Из теории Френеля следует, что в том случае, когда в пределах отверстия или щели укладывается четное число зон Френеля, в центре экрана будет наблюдаться дифракционный минимум, поскольку волны будут гасить друг друга попарно, если нечетное – максимум, поскольку одна зона остается непогашенной и будет посылать свет в центр экрана.
Различают дифракцию Френеля и дифракцию Фраунгофера. Дифракция Френеля наблюдается в расходящихся лучах, а дифракция Фраунгофера в параллельных. Параллельные лучи можно получить, например, при помощи линзы, в фокус которой помещен точечный источник света. Узкий пучок параллельных лучей дают лазерные источники света.
 |
Рис.4. К выводу формулы координат минимумов и максимумов при дифракции на узкой щели.
согласно принципу Гюйгенса, является источником вторичных волн, которые будут распространяться за плоскостью щели по всем возможным направлениям. Таким образом, пучок параллельных лучей, проходя через щель, дифрагирует под всевозможными углами j, изменяющимися в пределах от 0 до p/2.
Вторичные волны за плоскостью щели можно сгруппировать в параллельные пучки, из всей совокупности которых на рис. 4 представлены только два. Пучок I распространяется без изменения направления. Этот пучок собирается линзой Л в ее главном фокусе – в точке O (при использовании лазера линза не требуется). В точку O световые колебания приходят в одной фазе, т.к. их разность хода равна нулю, поэтому в точке O будет наблюдаться яркий максимум нулевого порядка (яркое изображение щели).
Пучок II отклоняется от первоначального направления под углом дифракции j. Он собирается линзой в побочном фокусе – точке P. Чтобы определить световой эффект в этой точке, воспользуемся методом зон Френеля. Разобьем фронт волны AB системой параллельных плоскостей, перпендикулярных к направлению лучей и отстоящих друг от друга на расстоянии l/2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.