Основы теории делимости
Пусть есть a,bÎZ
N,Z,Q,R,C – множества чисел
Теорема: о делимости целых чисел
Для любых a,bÎZ существуют единственные q, r такие, что 0<=r<|b| a=bq+r
q=[a/b] r={a/b}
Если r=0, то a||b (a кратно b)
Теорема 1: Свойства деления
1) a||b, b||c => a||c (транзитивность)
2) a1,a2, … ,ak | => "l1,l2, … , lk
ai||c |
Ski=1aili||c
Если любое а кратно с, то линейная комбинация тоже кратно с
Существует max(a,b)<=M(a,b)<=ab
Определение:
Существует a,b a||d, b||d D(a,b) – НОД
1<=D(a,b)<=min(a,b)
Определение:
a,b называются взаимно простыми, если M(a,b)=1
Теорема 2: Свойства НОД и НОК
1) a1,a2, … ,ak
m||a1, m||a2, … , m||ak m||M(a1,a2, … ,ak) НОД||НОК
Доказательство: Пусть m=M(a1,a2, … ,ak)q+r 0<r<M(a1,a2, … ,ak)
r=m-M(a1,a2, … ,ak)q => r||a1,a2, … ,ak (т.к. m||a1,a2, … ,ak) =>наше предположение неверно r=0
2) a1,a2, … ,ak d1,d2, … ,dk
D(a1,a2, … ,ak)=M(d1,d2, … ,dn)
Доказательство: ai||d1, ai||d2, … , ai||dn т.е. аi – кратное
ai||M(d1,d2, … ,dn), M(d1,d2, … ,dn)||dj
3) ab=D(a,b)×M(a,b)
Доказательство: ?????
Пусть есть a1,a2, … ,ak
Как найти D(a1,a2, … ,ak)?
Пусть D(ai,aj) известно, тогда
d1=D(a1,a2); d2=D(d1,a3); dk-1=D(dk-2,ak)
Утверждение:
ab||c и (a,c)=1 => b||c
Определение:
а называется простым если а||a или a||1 и у него нет других делителей.
Теорема: 3 Свойства простых чисел.
1) a,p (p – простое) a||p или a||b (b,p)=1
2) ab||p => a||p или b||p
3) a¹1, существует простой делитель
p=min{d1,d2, … ,dk} – простое
a=p1p2…pk=paqbrc (p,q,r – простые числа)
Доказательство:
1) a=a1p1, если а1>1, то a1=a2p2
2) Существует единственная комбинация разложения числа на простые сомножители, a=p1p2…pk=q1q2…qk (p,q – простые)
По теореме 3 – pi||q1, pj||q2
Нахождение простых чисел в интервале от 1 до N
Алгоритм:
S1 p1=2, k=1
k+1 Pk
Pk>N остановка, числа можно просматривать до ÖN или до [ÖN]+1
Теорема: 5 Евклида
Множество простых чисел бесконечно
Доказательство: Пусть множество конечно {p1,p2…pk}
Следующее простое число это произведение предыдущих плюс 1, т.е.
pk+1=p1p2…pk+1
Дано: aÎZ a=paqbrc…
{p1,p2…pk}
2=p1<p2<…<pk
k,i Step0 k=1, i=1
Step1 a=1 => stop
a=pkq+r if r=0 => Step3
Step2 r=0 di=pk, i=i+1 => Step1
Step3 r¹0 k=k+1 => Step1
Алгоритм Ферма
a=xy, a=u2-v2=(u-v)(u+v)
R(u,v)=u2-v2-a остановка при R(u,v)=0
R(u,v)<0 V=V+1
R(u,v)>0 U=U+1
R(u+1,v)=(u+1)2-v2-a=u2-v2-a+(2u+1)=R(u,v)+2u+1
R(u,v+1)=u2-(v+1)2-a=u2-v2-a-(2v+1)=R(u,v)-2u-1
Алгоритм Евклида и цепные дроби.
D(a,b) - ?
D(a,b)=D(a-bq,b) a-bq+r
a=bq0+r0 D(b,r0)
b=r0q1+r1 D(r0,r1)
r0=r1q2+r2 D(r1,r2)
… … …
rk-2=rk-1qk+rk D(rk-1,rk)
rk-1=rkqk+1
a) a,b – четные => D(a,b)=2D(a/2,b/2)
b) a – четное, b – нечетное => D(a,b)=D(a/2,b)
c) D(a,b)=D(a-b,b)
d) a,b – нечетные => a-b – четное
e) |a-b|<max{a,b} a,b>0
S1 k=0
k=k+1, a=a/2, b=b/2 (пока a,b четные)
S2 a – нечетное => tmp=-b goto S4
а – четное => tmp=a
S3 tmp=tmp/2
S4a if (tmp – четно) => goto S3
S4 if (tmp>0) then a=tmp
Else b=-tmp
S5 tmp=a-b
Tmp=0 stop
D(a,b)=2ka
Goto S3
Пример:
a b tmp
76501 29719 -29719
76501 29719 40782 23391
23391 29719 -6328 -3164 -1522 -791
23391 791 22600 11300 5650 2825
2825 791 2034 1017
1017 791 226 113
113 791 –678 -229
113 339 -226 -113
113 113
a>b
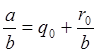
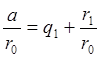
. . .
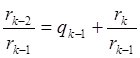
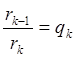
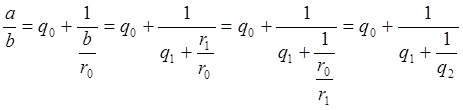
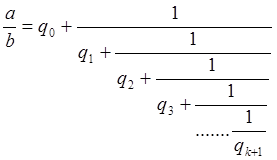
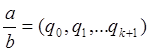
a<b
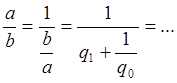
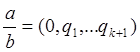
a/b<0
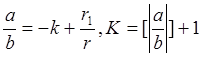
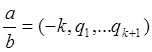
Теорема: 6
Любое рациональное число можно разложить в цепную дробь, одним и только одним способом, где все qi>0, i>=1, a последнее qk>1
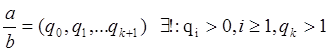
(Если qk не >1 то 2 разл: (q0,q1,…,qk-1,1)
ZÎR имитируем алгоритм Евклида для вещественного числа
Z=q0+b1 q0=[Z] – выделим целую часть числа
b1Î(0,1), Z1>1
Z=q0+1/Z1 (разложение числа в цепную дробь)
Z1=q1+b2 q1=[Z1]
b2Î(0,1)
Z1=q1+1/Z2, Z2>1
Z2=q2+b3
….
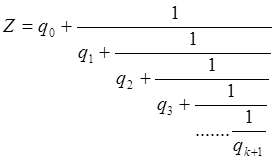 =q0,q1…qk+1
=q0,q1…qk+1
Пример:
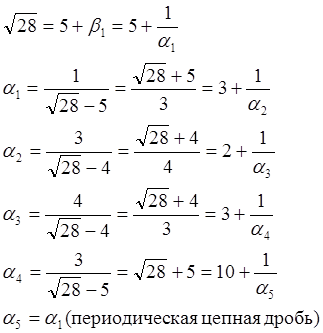
(5,(3,2,10)) т.е. цепная периодическая дробь
a=bq0+r0
b=r0q1+r1
r0=r1q2+r2
… …
rk-2=rk-1qk+rk
rk-1=rkqk+1
D(a,b)=rk=rk-2 -rk-1qk=rk-2-(rk-3-rk-2qk-1)qk=…=ax+by
(1) y0=0, y1=1, yi+1=yi-1-qk+1-i
D(a,b)=axk+2+byk+2
Xi+1=yi
d=ax+by
76501=29719 2+17063
29719=17063 1+12056
17069=12056 1+4407
12056=4407 2+3842
4407=3842 1+565
3842=565 6+452
565=452 1+113
453=113 4
76501x+29719y=113
по формуле 1 находим y
d 1 6 1 2 1 1 2
y 1 –1 7 –8 23 –31 54 –139
y=-139 x=54
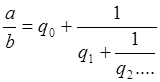 обрываем
процесс на 1 шаге, 2 и т.д.
обрываем
процесс на 1 шаге, 2 и т.д.
d0=q0
d1=q0+1/q1…
d2=q0+1/q1+1/q2… подходящие дроби
dk=-Pk/Qk – подходящая дробь
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.