Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 2

Найдем формулы для вычисления P_k  Q_k

Вводим условную дробь  d_-1=1/0 т.е. P_-1,Q_-1=0

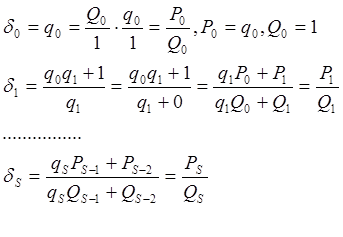
		1	2	3	4	5	6	7	8
Qs		2	1	1	2	1	6	1	4
Ps	1	2	3	5	13	18	121	139	677
Qs	0	1	1	2	5	7	47	54	263

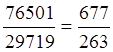
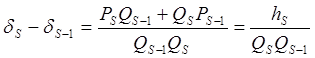
h_s=P_sQ_s-1-Q_sP_s-1

(q_sP_s-1+P_s-2)Q_s-1-(q_sQ_s-1+Q_s-2)

P_s-1=P_s-2Q_s-1-Q_s-2P_s-1=-(Q_s-2P_s-1-P_s-2Q_s-1)=-h_s-1

h_s=-h_s-1=(-1)²h_s-2=…=h₀(-1)^s

h₀=-1, h_s=(-1)^s+1

;   

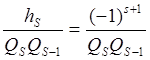Q_-1=0; Q₁=1; Q₂=q₂Q₁+Q₀  (последующие Q_i монотонно возрастают)

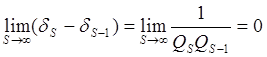
h_s=(-1)^S+1=(Q_s-1P_s-P_s-1Q_s)

P_sQ_s  ||  d     делятся на d=1

D(P_s-2,Q_s)=1  взаимно просты

aÎR

a=q₀+b₁     q₀=[a]

a₁=q₁+b₂     q₁=[a₁]

......

a_S=q_S+b_S+1

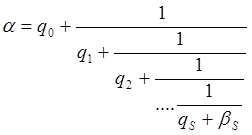
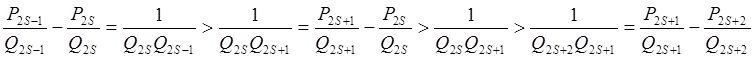
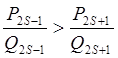 подпоследовательность нечетных дробей убывает

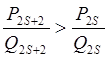 подпоследовательность четных дробей возрастает

; 

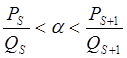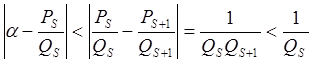
=(5,(3,2,3,10))    =5,29150267

0,0001    1/Q_S²<0,0001   => Q_S>100

		1	2	3	4	5	6	7
Qs		5	3	2	3	10	3	2
Ps	1	5	16	37	127	1037	4018	9403
Qs	0	1	3	6	24	247	465	1777

16/3=5,3(3)

37/7=5,2857

127/24=5,2915

1037/247=5,2915

Теорема: №7

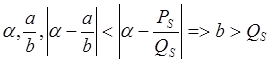
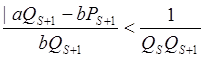
Пусть b<=Q_s=>bQ_s+1<=Q_s+1Q_s=>|a Q_s+1-b P₊₁|<1 = 0

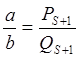;   b<=Q_s+1>Q_s

Диафантовы уравнения

ax+by=c    a,b,c,x,yÎZ   x,y - ?

Теорема: 8

d=D(a,b) уравнение ax+by=c разрешимо <=> c||d при этом множество решений описывается следующими уравнениями

x=x₀-(b/d)t

y=y₀-(a/d)t     tÎZ

Если существует (x₀,y₀) – частное решение.

Доказательство:

1)  Существует если a||d то b||d , тогда есть решение если c||d

Пусть a=de₁; b=de₂; c=de₃  =>  ax₀+by₀=d имеет решение – x₁,y₁

a(e₃x)+b(e₃y)=c  решение есть - (e₃x, e₃y)

2)  Пусть существует x₀,y₀ : ax₀+by₀=c

a(x-x₀)+b(y-y₀)=0 <=>  Числовое тождество <=> (a/d)(x-x₀)=-(b/d)(y-y₀)

((a/d);(b/d))=1 (иначе d не НОД)

-(b/d)(y-y₀)|| (a/d)        => y-y₀=(a/d)t  =>  y=y₀+(a/d)t

аналогично x=x₀+(b/d)t, т.е. если существует решение x,y то отношение имеет такой вид.

Доказательство в обратную сторону, в результате подстановки получается тождество.

Дополнение: ax+by=c разрешимо, если D(a,b)=1

Пример 1:

15x+19y=1

19=15 1+4

15=4 3+3

4=3 1+1

3=1 3

q       1   3   4

0  1  -1   4  -5

x₀=-5     x=-5+19t

y₀=4       y=-(-4+15t)

126x-102y=18

D(126,102)=6

21x-3y=3

ax+by=D(a,b)

Решим 21x-17y=1 для этого решим 21x+17y=1

21=17 1+4

17=4 4+1

4=4 1

q      4  1

0  1 –4  5

21(+4)-17(+5)=1

21(-4)-17(-5)=1

x₀=-5     x=-4 3=12

y₀=-4       y=-5 3=15

Общее решение : x=-12+17t

Теорема: 9

a₁x₁+a₂x₂+…+a_nx_n=С <=>  С||D(a₁a₂ …a_n)  Если ???||D => С||D

Доказательство:

1) C=d c   По методу математической индукции

a₁x₁+a₂x₂+…+a_nx_n=d =D(a₁a₂ …a_n)

докажем, что всегда разрешимо при любых n.

n=2 a₁x₁+a₂x₂=d =D(a₁,a₂)  разрешимо (база)

2) Индукционный переход. Докажем для n+1

a₁U₁+a₂U₂+…+a_nU_n+a_n+1U_n+1 =D(a₁a₂ …a_n, a_n+1)=D(d, a_n+1)=d

dy+a_n+1U_n+1=d

_   _                     _       _             _

(y, U_n+1), где d=a₁x₁+a₂x₂+…+a_nx_n

a₁(y,`x<sub>1</sub>)+a<sub>2</sub>(y, `x₂)+…+a_n(y, `x_n)+ a_n+1U_n+1=d

Сравнение

a,bÎZ   ,   m

a=b(mod m)  |

a=b(m)          |        Отклонение по модулю m

b=<a>m         |

(a-b) || m        |

Существует множество А – это есть АхА={(a,b)| a,bÎA}

RÌAxA

R – бинарное отклонение на множестве А – это подмножество произведения декартовых множеств.

a R b

(a,b)ÎR

a встепает в отношение с b, если (a,b)ÎR

m – фиксированный модуль

Декартово произведение – множество пар

Выделим множество R, если два предм. a,b входят в R, то они вступают в отношение R (а вступает в отношение с b)