Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 6

R_n-1(x)=R_n(x) Q_n+1(x)

Пример:

D(x⁴+x³-3x²-4x-1, x³+x²-x-1)  типовая задача

n=4, m=3, k=1

1  1 -3 -4  1           1  1 –3  –4   1

a₄ a₃ a₂ a₁ a₀              1   1 –1  –1

0 –2  –3   -1

-2   -3   -1

r₁=a₄/b₃=1

a_j=a_j-b_j-1^.r₁

r₀=a₃/b₃=0

a_j=a_j-b_j-1^.(j={2,1,0})

x⁴+x³-3x²-4x-1=(x³+x²-x-1)(x+0)+(-2x²-3x-1)

(x³+x²-x-1)=(-2x²-3x-1)(-x/2+1/4)+(-1/4x-1/4)

(-2x²-3x-1)=(-1/4x-1/4)(8x+4)+0

НОД:  x+1

Q_m(x)=x-c

Схема горнера:

m=1 ; b₁=1, b₂=-c

k=n-1, n-2, … ,0

Z_k=a_k+1  ;  a_k=a_k+1

P(x)=Q(x)(x-c)+r

r=P(c)

P_n=Q₀+a₁x+a₂x²+…+a_nxⁿ=(a_nx+a_n-1)x+a_n-2)x+a_n+3)

d(x)=D(P(x),Q(x))=>Существует единственные U(x),V(x):P(x)U(x)+Q(x)V(x)=d(x)

(доказывается обратным ходом алгоритма Евклида)

v₀(x)=0

v₁(x)=1

….

V_i+1(x)=v_i-1(x)-Q_k+1-i(x)v_i(x)

v(x)=v_k+2(x)

u(x)=v_k+1(x)

d(x³-2, x²-3x+2)=x³-2=(x²-3x+2)(x+3)+7x-8

x²-3x+2=(7x-8)((1/7)x-(13/49))-6/49

7x-8=-6/49(-943/6x+169/3)+0

D(x³-2, x²-3x+2)=1

		(1/7)x-(13/49)	X+3
0	1	-(1/7)x+(13/49)	(1/7)x2+(9/49)x+(10/49)

-(6/49)=(x³-2)(-(1/7)x+(13/49))+(x²-3x+2)( (1/7)x²+(9/49)x+(10/49))

Теорема: 23 Китайская теорема об остатках для многочленов

Существует P₀(x), P₁(x),…,P_k-1(x) : (P_i(x),P_j(x))=1, i+j

<S(x)>_Pi(x)=U_i(x)  (*)   -  китайский код многочлена

u_i=deg(P_i(x)

N=n₀+n₁+…+n_k-1

Существует единственный S(x): deg S(x)<N, который удовлетворяет (*)

Доказательство:

C(x)=П_i=0^k-1P_i(x)

C_j(x)=C(x)/P_j(x)

<D_j(x)C_j(x)>_Pj(x)=1          (M_ix_i=1(m_j)

S(x)=<S_i=0^k-1D_i(x) C_i(x) U_i(x)>_C(x)

Пример:

P₀(x)=x²-2

P₁(x)=x²-3x+2

U₀(x)=1, U₁(x)=1

C(x)=(x³-2)(x²-3x+2)=x⁵-3x⁴+2x³-2x²+6x-4

C₀(x)=x²-3x+2

C₁(x)=x³-r

<D₀(x), C₀(x)>_Po(x)=1

<D₁(x), C₁(x)>_P1(x)=1  =>  D₀(x) (x²-3x+2)=1(x³-2)

D₀(x)=(-7/6)x²-(4/3)x-(5/6)

D₁(x)=(-7/6)x-(13/6)

S(x)=P₀(x)D₀(x)+ P₁(x)D₀(x)

Частный случай теоремы 23

X1	X2	…	Xn
y1	y2	…	yn

x_i¹y_j

S_i(x) : S_i(x)=y_i i=1,2…n

S(x) – многочлен проходящий через все узлы интерполяции – (x_i,y_i)

<S(x)>_X-Xi=y_i   -  остаток от деления S(x) на (x-x_i) (Схема Горнера)

S(x)=(x-x_i)+c

C(x)=(x-x₁) (x-x₂)… (x-x_n)

C_i(x)=(      ) (x-x_i-1) (x-x_i+1)…

<D_i(x)C_i(x)>_X-Xi =1

<D_i(x) (x-x₁) (x-x₂)… (x-x_i-1) (x-x_i+1)… (x-x_n)>_X-Xi =1

D_i(x) (x-x₁) (x-x₂)… (x-x_i-1) (x-x_i+1)… (x-x_n)=1

S(x)=S_i=1ⁿD_i(x) C_i(x) U_i(x)=S_i=1ⁿy_i   -   Многочлен Лагранжа

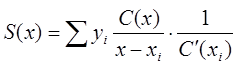
Через n точек можно провести многочлен deg<=n-1

Недостаток: При добавлении данных надо пересчитывать весь многочлен.

Интерполяционный метод Ньютона.

Подход:

X1	X2	…	Xn
y1	y2	…	yn

S₁(x)  S₂(x) … S_n(x)       (x-x₁)

S₁(x)=y₁                          (x-x₂)

….                                     …

S_k(x)-S_k-1(x)                              (x-x_k-1)

x₁,x₂….x_k-1

*  a||b₁ и a||b₂  (b₁;b₂)=1  =>  a||b₁b₂ 

по аналогии с * 

S_k(x)-S_k-1(x)||(x-x₁)(x-x₂) … (x-x_k-1)

S_k(x)-S_k-1(x)=A_k(x-x₁)(x-x₂) … (x-x_k-1)

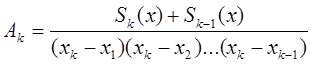
S_n(x)=A₁+A₂(x-x₁)+A₃(x-x₁)(x-x₂)+…+A_n(x-x₁)(x-x₂) … (x-x_n-1)

y₁=A₁ |  x=x₁

y₂=A₁+A₂(x₂-x₁)  |  x=x₂

Пример:

x₁    x₂    x₃

-1     0     1

y₁    y₂    y₃            S₃(x) =A₁+A₂(x-x₁)+A₃(x-x₁)(x-x₂)

3     -1    2              3=A₁  |    x=-1

-1=A₁+A₂(1)  |  x=0  |  A₂=-4

2=A₁+A₂(2)+A₃(2)(1)  |   A₃=7/2

S₃(x)=3-4(x+1)+7/2(x+1)x

S₄(x)=S₃(x)+A₄(x-x₁)(x-x₂)(x-x₃)

Приближенная интерполяция

F(x₁,x₂…x_n)

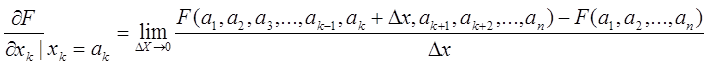
F(x,y)=sin x^.cos x или F(x,y,z)=x²z+xy+xy²z³

;       

;     

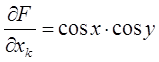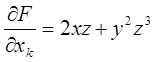
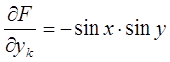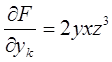
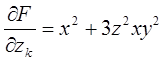
Метод наименьших квадратов

S(x_k)-y_k=Dk

S_k=1ⁿDk  àmin

S_m(x)=a₀+a₁x+a₂x²+…+a_mx^m

S_k=1ⁿDk²  =S_k=1ⁿ(a₀+a₁x+a₂x²+…+a_mx^m)²

Ф(a₀,a₁,…,a_m) àmin  {a₀,…,a_m}

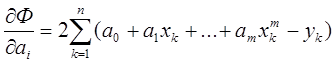
Пример:

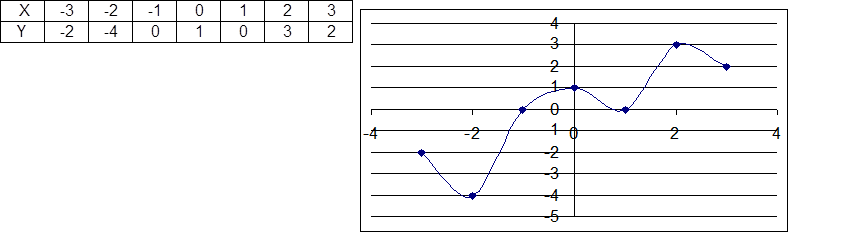F(a,b)=ax+b

S_k=1⁷(ax_k+b-y_k)²=Ф(a,b)

;

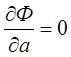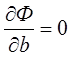
Ф(a,b)=(-3a+b+2)²+(-2a+b-4)²+(-a+b)²+(b-1)²+(a+b)²+(2a+b-3)²+(3a+b-2)²

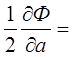(-3a+b+2)(-3)+(-2a+b-4)(-2)+(-a+b)(-1)+(b-1)(0)+(a+b)(1)+(2a+b-3)(2)+(3a+b-2)(3)=0

Комбинаторика

Определение: способ размещения в определенном порядке некоторого числа элементов. Суммы S называют размещения.

S={a,b,c}

{ab,ac,ba,ca,bc,cb}

{ab,ac,bc}