Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 11

По теореме 32 любая разность в (*) можно записать в виде функции.

(*) <=> f(x+k)+P₁(x)f(x+k-1)+P₂(x)f(x+k-2)+…+P_k(x)f(x)-Q(x)=0

f(x+k)+ S^k_s=1 P_s(x)f(x+k-s)=Q(x) (1)        Если Q(x)=0  (1*)

D³f(x)+3Df(x)+2f(x)=0

f(x+3)+3f(x+2)=0

Лемма:  Любое решение такого уравнения k-го порядка определяется набором k функций

{f₀, f₁,…,f_k-1}

Доказательство:

?????????

Теорема: 33

Если f₁(x), f₂(x)…f_p(x) – решение (1*), то их линейная комбинация, тоже решение (1*) j(x)=S^p_i=1 C_if_i(x)

f(x+k)+S^k_s=1 P_s(x)f(x+k-s)=0

P₀(x)=1

S^k_s=1 P_s(x)f(x+k-s)=0

S^k_s=1 P_s(x)j(x+k-s)= S^k_s=1 P_s(x) S^p_i=1 C_if_i(x)= S^p_i=1 C_i S^k_s=1 P_s(x) f_i(x)

S^k_s=1 P_s(x) f_i(x)=0

Теорема: 34

Известно k решений (1*): f₁(x),…,f_k(x)

D[f₁(0),…,f_k(0)]¹0

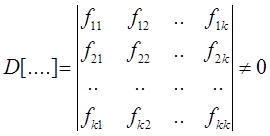  f_ij=f_j(i-1)

f(x)=S^k_i=1C_if_i(x)

Доказательство:

Если функция представлена в виде f(x)=S^k_i=1C_if_i(x), то по теореме 33 она является решением.

Пусть f(x) – решение, по лемме существуют {f_0, f₁…f_k-1}

Рассмотрим {j(x)=S^k_i=1C_if_i(x)}

Выберем j(x) такую, что она совпадает с f(x) в k точках {f_0, f₁…f_k-1}

j₀= j(0)= C₁f₁₁+C₂f₁₂+…+C_kf_1k=f₀

…….

j_k-1= j(k-1)= C₁f_k1+ C₂f_k2+…+C_kf_kk=f_k-1

Получаем систему линейных уравнений с определителем ¹0 => существует тривиальное решение => можно найти C_i , т.е. любое решение представимо в таком и только таком виде f(x)=S^k_i=1C_if_i(x)

Определение:

Набор решений уравнения (1*) {f₁(x)…f_k(x)}

Называется линенонезависимым, если линейная комбинация для любых С_i

S^k_i=1C_if_i(x)=0   при S |C_i|¹0

????

Теорема: 35

Если {f₁(x)…f_k(x)} … ЛНЗ, то D[…]¹0 (Теорема 34)  (Обратное неверно)

Теорема: 36

Рассмотрим уравнения (1), (1*):

Их общее решение можно представить в виде суммы частного решения (1) и общего решения (1*)

Доказательство:

Пусть известно решение (1) f*(x) и набор решений {f₁(x),…,f_k(x)}, т.е. известны все решения (1*)

D[f₁(0)…f_k(0)]

Тогда: f(x)=f*(x)+S^k_i=1C_if_i(x)

Очевидно, что любая функция представленная в таком виде, является решением (1), f(x+k)=S^k_S=1P_s(x)f(x+k-s)=Q(x)

Рассмотрим произвольное решение (1) f(x)=f*(x)+j(x)

Подставим f(x) в (1): S^k_s=0P(x)[f*(x+k-s)+j(x+k-s)]=Q(x)

S^k_s=0P(x)×f*(x+k-s)+S^k_s=0P(x)×j(x+k-s)]=Q(x)   и S^k_s=0P(x)×f*(x+k-s)=Q(x)  =>  S^k_s=0P(x)×j(x+k-s)]=0

Частный случай: Линейные рекуррентные однородные уравнения порядка k с постоянными коэффициентами

F(x+k)+a₁f(x+k-1)+…+a_kf(x),  a_iÎR

Будем искать решения в виде f(x)=l^x

l^x+k+l^x+k-1×a₁+…+l^xa_k=0  :   l^x¹0

l^k+l^k-1×a₁+…+a_k=0  - характеристическое уравнение, линейного рекуррентного однородного уравнения порядка k.

Теорема: 37

Если все корни характеристического уравнения различны {l₁,l₂,…,l_k: l_i¹l_j}, то линейно независимое решение линейного рекуррентного однородного уравнения порядка k представимо в виде.

{l₁^x,l₂^x,…,l_k^x}

=

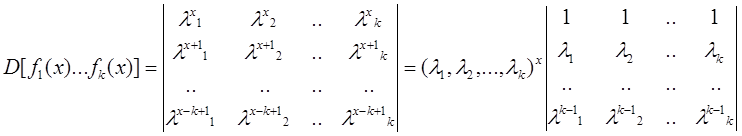=(l₁,l₂,…,l_k)^x×P_i>j(l_i-l_j)

Доказательство:  (от противного)

Пусть существуют не тривиальные C_i : S^k_i=1C_if_i(x)=0   "x=0,1,…,k-1

l^x¹0, если l_k=0, то по теореме Виета для характеристических уравнений

a_k=l₁…l_k  =>  l_k=0

f(x+k)+a₁f(x+k-1)+…+a_k-1f(x+1)=0,  т.е. если l_k=0, то уравнение ?????????

f(x+k)+a₁f(x+k-1)+…+a_kf(x)=0

l^k+a₁l^k-1+…+a_k=0  -  существует k корней

{l₁^x,l₂^x,…,l_k^x }

C₁l₁^x+C₂l₂^x+…+C_kl_k^x

Если все корни различны.

Пусть существует l_iÎC   l_i=r e^ij=r(cos j+i Sin j)=>

существует l_jÎC   l_j=`l_i =r(cos j-i Sin j)  (если вещественные коэф)

C_il_i^x,C_jl_j^x – можно заменить на

С_i r^x(cos xj), С_j r^x(sin xj),  а система решений останется линейно независимой

Теорема: 38

Пусть l^k+a₁l^k-1+…+a_k=0   имеет корни различной кратности

l₁ – p₁; l₂ – p₂ ; … ; l_n – p_n

p₁+p₂+…+p_n=k

Любой корень дает столько решений, какова его кратность

Пример: l₁={l₁^x, xl₁^x, x²l₁^x,…, x^P1-1l₁^x,

l₂^x, xl₂^x, x²l₂^x,…, x^P2-1l₂^x,

….        …         …   …

l_n^x, xl_n^x, x²l_n^x,…, x^Pn-1l_n^x}

Чтобы решить однородное уравнение:

1)  Найти характеристическое уравнение

2)  Найти все его корни

Нахождение частного решения неоднородного уравнения

Частный случай : правая часть многочлен.

f(x+k)+a₁f(x+k-1)+…+a_kf(x)=Q(x)

l^k+a₁l^k-1+…+a_k=0  (*)

Q(x)=C₀+C₁x+…+C_nxⁿ

Пусть первый корень кратности S уравнения (*)  S>=0