Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 14

Соединим a₀ и a₁ ребром, попадаем в т. 47, по т. 47 связанный и все вершины четные. Удаляя ребро получим нечетные а₀ и а₁.

Алгоритм построения Эйлеровой цепи.

Списки инцидентности.

Каждой вершине сопоставим список, в этом списке все вершины смежные с данным ребром.

[v]   VàV₁àV₂à…

Для изолированной вершины пустой список.

Граф – это массив списков.

  [V₁] à         Для неориентированного графа ребро (V₁,V₂) графа вершина в V₁ и

[V₂] à         эта же вершина V₂ может быть список списков.

….

[V_n] à

Из произвольной вершины идем к смежной и это ребро удаляем и.т.д. т.к. все вершины четные, то мы вернемся в V₀ и заносим вершину в маршрут, а из стека удаляем, переходим к следующей вершине в стеке.

Списки инцидентности

S1   SE={Æ}   сюда будем заносить вершины, заносим все подряд.

Stack={V}

S2 If Stack – пуст Stop  Граф имеет Эйлерову цепь

S3 else  V:=top(stack) – Вытаскиваем верхний элемент

If (SI[V]¹0) U:=SI[V];  Список инцидентности, не пуст, то вытаскиваем элемент

Del(U,V) в списке для U удаляем V, а в списке для V удаляем U и заносим в стек

Если SI[V]=0, то Và SE{} и V удаляем из стека.   

Пример:

4

             3

5

1                                                 6

⁸

2

7                9

Список Инцидентности

1à2à3

2à3à7à8

3à1à2à4à5

4à3à5

5à3à4à6à8

6à5à7à8à9

7à2à6à8à9

8à2à5à6à7

9à6à7

Stack  1   2,1     3,2,1      1X,3,2,1    4,3,2,1   5,4,3,2,1   3X,5,4,3,2,1  6,5,4,3,2,1

SE     0     0        0             1                 1              1                 1,3                1,3

Stack  7,6,5,4,3,2,1     2,7,6,5,4,3,2,1   8,2,7,6,5,4,3,2,1   5X,8,2,7,6,5,4,3,2,1

SE            1,3                      1,3                    1,3                            1,3,5

Stack  6,8,2,7,6,5,4,3,2,1   9,6,8,2,7,6,5,4,3,2,1    7,9,6,8,2,7,6,5,4,3,2,1

SE            1,3,5                             1,3,5                               1,3,5

Удаляем весь стек   SE   1,3,5,8,7,9,6,8,2,7,6,5,4,3,2,1

Деревья

Определение: Связанный граф не содержащий циклов называется деревом.

Просто граф не содержащий циклов, называется лесом.

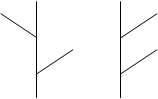
   Дерево                                        Лес

Теорема: 48

Граф является деревом тогда и только тогда, когда между его двумя вершинами существует одна и только одна цепь.

Доказательство:

Граф – дерево, тогда граф связан и две вершины можно соединить цепью, пусть есть две цепи, тогда из них, можно построить цикл (следствие 2, теорема 43) и наоборот.

Теорема: 49

Дерево содержащее не менее двух вершин имеет, по крайней мере 2 концевые вершины (DegV<1).

Доказательство: Рассмотрим максимальную цепь:

a₀x₁a₁x₂…x_La_L

Докажем, что deg a₀ и a_L =1

Пусть deg a_L>1, тогда из нее есть ребро a_L+1, x_La_L причем a_L+1¹a_i, иначе получился бы цикл, это не дерево => максимальная цепь удлиняется, значит deg a_L>1, тоже для а₀.

Лемма: После удаления из дерева концевой вершины вместе с ребром получается дерево.

 

Теорема: 50 Дерево с Р вершинами имеет Р-1 ребро.

Доказательство: Индукция по P:

1. P=1   -   0 ребер.

2. Индукционный переход   Пусть P<=k верно

Докажем для k+1>=2.

Дерево не более двух вершин или 2 концевые вершины (т. 49) по лемме одну концевую вершину убираем, тогда получим,

Для k вершин  -  k-1 ребро

+                     +

1                     1

k+1 вершин  -  k ребер

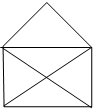
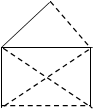
Определение: Дерево в графе, которое содержит, все его вершины называется каркасом данного графа (стягивающее дерево, покрывающий граф)

Т.е. ребра, которые надо оставить, чтобы сохранилась связанность.

 

каркас

Теорема: 51 В связанном графе существует по крайней мере 1 каркас.

Доказательство:

1)  Если в связанном графе нет циклов, то это дерево.

2)  Если есть циклы, то удаляем любое ребро из цикла, пока не кончиться цикл.

Пример, построения графа в глубину.

{(V,U)}  идет в каркас, мы обойдем все вершины и у нас будет каркас( т.к. не будет циклов), мы не возвращаемся обратно в вершину.