Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 10

Разбиение чисел

Число n=b₁+b₂+…+b_k   b_i>0, n>0  b_i могут повторяться

n=a₁+a₂+…+a_k

a₁>=a₂>=…>=a_k

Упорядочены по убыванию

P(n,k) – число разбиений числа n на k слагаемых

P(n)=Sⁿ_k=1 P(n,k) – число всевозможных разбиений

P(0,0)=P(0)=1

P(6)=11

6

5+1

4+2

4+1+1

3+3

3+2+1

3+1+1+1

2+2+2

2+2+1+1

2+1+1+1+1

1+1+1+1+1+1

n=a₁+a₂+…+a_k

Диаграмма Ферререса

Строиться для каждого разбиения числа n

16=6+4+4+2

×  ×  ×  ×  ×  ×   a₁

×  ×  ×  ×                    a₂

×  ×  ×  ×                    a₃

×  ×                a₄

Можно транспонировать

16=4+4+3+3+1+1

×  ×  ×  ×          a₁

×  ×  ×  ×                    a₂

×  ×  ×             a₃

×  ×  ×             a₄

×                   a₅

×  a₆

Теорема: 30 Число разбиений числа n на k слагаемых = числу разбиений с максимальным элементом k

P(n,k)=

Доказательство:

????

Теорема: 31 Число разбиений числа n попарно различные слагаемые = числу разбиений числа n на нечетные слагаемые

Доказательство: Возьмем произвольное разбиение на нечетные слагаемые

n=b₁+b₁+…+b₁ + b₂+b₂+…+b₂  +…+  b_p+b_p+…+b_p

r₁                      r₂                                r_p

b_i – нечетные

Возьмем r_i и возьмем двоичное разложение числа (столько раз встречается b_i)

r_i=2^q1+2^q2+…+2^qp

(q₁>q₂>…>q_p)

b_p+b_p+…+b_p    b_i×2^qi

r_p

b_i×2^q1+b_i×2^q2+…+ b_i×2^qp   все они будут попарно различимы, т.к. b_i нечетно т.о. Каждому способу разложения на рациональные нечетные слагаемые = способ разложения на попарно различные слагаемые.

Пример:

26=7+5+5+3+3+1+1+1

26=7×2⁰+5×2¹+3×2¹+1×2¹+1×2⁰=7+10+6+2+1

n=c₁+c₂+…+c_l  оно старше n=a₁+a₂+…+a_k

Если существует p<=min{l,k}: c_i=a_i, i<p c_p<a_p

Противоположный лексикографическому

n=n

…

n=1+1+1+…+1

Просмотрим группу не единичных слагаемых

Пусть  t такое что d_t>1, a a_i=1,  i>t

n=a₁+a₂+…+a_t-1+(a_t+1+1+…+1)=S Сумма хвостовых элементов

l=d_t-1

S1   S₁=n, r₁=1;  d=1;      s[ ] s_i  r_i  - rhfnyjcnm d hfp,btyb

|                 \- число элементов в разбиении число элементов без учета кратности

S2  If (s1=1) stop

S3  sum:=0;

If (sd=1)

{ Sum:=sum+rd;

d:=d-1;

}

sum:=sum+Sd

rd=rd-1;

l=Sd-1;

if (rd>0) d=d+1;

Sd=l;

[rd=[sum/l];

l=<sum>_e;

if (l>0)

{d=d+1;

Sd=l;  rd=1}

Пример:

n=9; d=1

sum=0;  r₁=0  l=8

8+1

7+2

7+1+1

6+3

6+2+1

6+1+1

5+4

5+3+1

5+2+2

5+2+1+1

5+1+1+1+1

4+4+1

4+3+2

4+3+1+1

4+2+2+1

4+2+1+1+1

4+1+1+1+1+1

….

1+1+1+1+1+1+1+1

Производящие функции

Числовой ряд:  {a_i}^oo_i=0

S₀=a₀

S₀=a₀+a₁

S₀=a₀+a₁+a₂

…

S₀=a₀+a₁+a₂+…+a_n

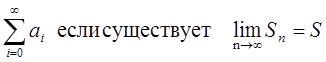
Говорят, что ряд сходиться если существует предел последовательно сти частных сумм, иначе ряд расходиться.

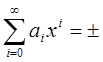   степенной ряд  +=S(x)

a₀,a₁,a₂,…,a_k

C₀ⁿ, C₁ⁿ… C_kⁿ  -  количество x элементных подмножеств

Сопоставляя комбинаторике последовательную функцию , которые называют производящей операции с рядами

А(х)=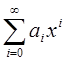

B(x)=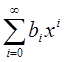

1)A(x)+B(x)=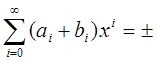

2)C×A(x)=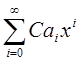

C_k=a₀b_k+a₁b_k-1+…+a_kb₀=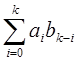  - произведение Коши

Примеры производящих функций для последовательностей

1)  {C_kⁿ}_k=0^oo

C_kⁿ=0,   k>n

Ряд:

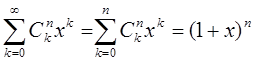
2)  1,2,4,8,…,2^k

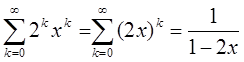    Пусть |x|<1/2

a⁰, a¹, a²,…,a^k,…

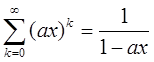   Пусть |x|<1/a

{F_n}^oo_n=0    F₀=F₁=1   F_n=F_n-1+F_n-2   n>=2

F(x)= =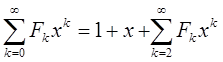

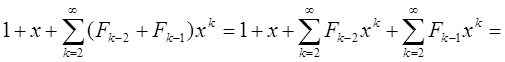
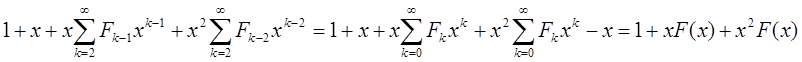
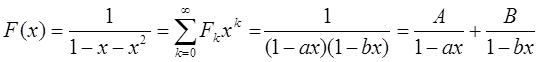
1-x-x²=0

x₁=(1/2)×(-1+Ö5)

x₂=(1/2)×(-1-Ö5)

1-x-x²=(x-x₁)(x₂-x)=-x₁x₂(1-x/x₁)(1-x/x₂)=*

a=1/x₁=2×1/(1+Ö5)

b=1/x₂=2×1/(1-Ö5)

*=(1-ax)(1-bx)

A=a/(a-b)    B=-b/(a-b)

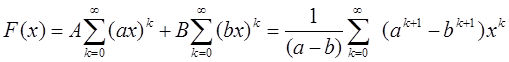
F(x)=

F_k=1/(a-b)×(a^k+1-b^k+1)=1/Ö5 [((1/2)×(1+Ö5))^k+1-((1/2)×(1-Ö5))^k+1]  Формула Бине

Рекуррентное уравнение

(Уравнение в конечных разностях)

f(x) – определим на множестве натуральных чисел x=0,1,2,…f(x)

f(0),f(1),f(2),…

f₀ f₁ f₂ … f_n=f(n)

Конечные разности

Df(x)=f(x+1)-f(x)

D²f(x)=Df(x+1)-Df(x)

D³f(x)=D²f(x+1)-D²f(x)

…              …         …

D^kf(x)=D^k-1f(x+1)-D^k-1f(x)

Это аналог производных

Свойства конечных разностей:

Теорема: 32

1) D^pf(x)=S^p_i=0(-1)^p-iC_i^pf(x+1)

2) f(x+p)=S^p_k=0C_k^pD^kf(x)

Линейные рекуррентные уравнения порядка k

Определение:

D^kf(x)+a₁(x) D^k-1f(x)+…+a_k(x)f(x)=Q(x)   (*)

Для любого i, а_i(x) известно => f(x)

Если Q(x)=0, то уравнение называется однородным в противном случае, оно называется неоднородным.