Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 7

A_kⁿ=n(n-1)(n-2)…(n-k+1)

A_nⁿ=Pⁿ-n!

C_kⁿ=A_kⁿ/P^k=n!/(n-k)!k!

Свойства:

1)

2)  S_k=0ⁿC_kⁿ=2ⁿ

3)  S_k=0ⁿ(-1)^kC_kⁿ=0

4)  C_kⁿ=C_n-kⁿ

5)  C_kⁿ=C_k-1^n-1+C_k^n-1

6)  C₀⁰=C_nⁿ=1

Треугольник Паскаля:

С₀ⁱ, С₁ⁱ, … С_iⁱ   (x+y)ⁱ

1

1  1

1  2  1

1  3  3  1

1  4  6  4  1

1  5 10 10 5  1

7)  Тождество Коши:

С_k^m+n=S_s=0^kC_s^mC_k-sⁿ

m=n=k

C_k^2k=S_s=0^k(C_sⁿ)²

Доказательство:

M,n,k – надо выбирать

S_s=0^kC_s^mC_k-sⁿ

Размещение и сочетание с повторениями.

n-k

A_kⁿ=n^k     n, n, n … n  - k раз

Сочетания

X={a₁,a₂,…a_n)

a₁   x₁   x_i>=0

a₂   x₂   x₁+x₂+…+x_n=k

..    ..

a_n   x_n

a_i  -  x_i+1  > 0

a₁a₁a₁| a₂a₂a₂|…|a_na_na_n|

x₁+1   x₂+1       x_n+1

C_n-1^n+k-1 

Принцип включения, исключения.

Задача: Существует S={x₁,x₂,…,x_n} – конечное множество

Существуют свойства p₁, p₂ … p_n – любой x_i может ими обладать.

N₍₀₎ – число элементов которые не обладают ни одним свойством.

N₍₁₎ – число элементов которые не обладают первым свойством.

N₍₁₂₎ – число элементов которые не обладают первым и вторым свойством.

…

N_(i1,i2,..in) – число элементов, которые обладают свойствами p₁, p₂ … p_n

1)  N₍₀₎ - ?  N₍₀₎=N-(N₍₁₎+N₍₂₎)+N_(1,2)

 

            1

                 2     S

Теорема: 24

N₍₀₎=N-S^N_i=1N_(i)+ S ^N_i1<i2N_(i1,i2)- S ^N_i1<i2<i3N_{(i1,i2,i3)+…+}(-1)^SS^N_i1<…<iSN_(i1,…,iS)+ (-1)^NSN_(1,2,…,N)

P(j,1), P(j,2),…,P(j,N)

1-C₁^r+ C₂^r- C₃^r+…+(-1)^rC_r^r=0

Перестановка в которой, ни один элемент не стоит на своем месте, называется беспорядком:

{1,2,3}   {2,1,3}    {3,1,2}  их число не бесконечно.

А_nⁿ=P_n

S={x₁,x₂,…,x_n}

|x|=n!

p₁,p₂,…,p_n; p_i – i-ый элемент стоит на своем месте, свойства перестановки.

N(i₁,i₂,…,i_r)=(n-r)! R свойств

SN(i₁,i₂)-C_rⁿ(n-r)!=n!/r!

N₍₀₎=n!-n!/1!+n!/2!-n!/3!+…(-1)ⁿn!/n!=n!(1-1+1/2!-1/3!+…(-1)ⁿ1/n!)=n!S_k=0ⁿ(-1)^k/k!

Кодирование с исправлениями (кодирование Хэмминга)

a=(a₁,…,a_n)     a_iÎ{0,1}

P<2_k^m   r – не более, чем в r разрядах могут существовать ошибки.

P – число слов.

a=(a₁,…,a_m)           | d(a,b)={a_i+b_i} – количество разрядов, которые не совпадают друг с   b=(b₁,…,b_m)          | другом. – Расстояние от a до b.

Пример:  a=(0,1,1,0)       |

b=(1,1,0,1)      |   =>  d(a,b)=3.  = функция расстояния между объектами

(A,B)ÎM  r(A,B)   M*M à R₊  (декартово произведение).

(1)  r(A,B)>0

r(A,B)=0  <=>  A=B

(2)  r(A,B)=r(B,A)

(3)  r(A,B)<=r(A,C)+r(C,B)

Докажем, что d(a,b) – расстояние т.е. обладает 1,2,3.

1)  очевидно

2)  очевидно

3)  d(a,b)<=d(a,c)+d(c,b)

a_i=b_i;   0<= …

a_i¹b_i;   1<= Пусть нет вклада a_i=c_i  |

c_i=b_i  |  =>  a_i=b_i  Значит наше предположение не                              верно a_i¹b_i;

Теорема: 26

S={a⁽¹⁾, a⁽²⁾, … , a^(p)} –

D(a⁽ⁱ⁾, a^(j))>=2r+1

a⁽ⁱ⁾ – передали i разрядное слово, не более, чем в r разрядах ошибка.

b – переданное слово.

Известно d(a⁽ⁱ⁾,b)<=r

A_i={b|d(a⁽ⁱ⁾,b)<=r  -  окрестность с центром в точке b.

b<Di

Окрестности не пересекаются:

Пусть это не так, тогда:

d(a⁽ⁱ⁾,w)<=r |  =>  d(a⁽ⁱ⁾, b⁽ⁱ⁾)<=d(a⁽ⁱ⁾,w)+d(a^(j),w)<=2+2=22 Значит наше предd(a^(j),w)<=r |        положение неверно.

 

.  .        

                .     .     .       слова

                                 Окрестность, любое слово на расстоянии <r стало P<rⁿ слов.

2^m, r  à  P?

A_i  aⁱ  A_i={a, d(a,aⁱ)<=r}

|A_i|=C₀^m+ C₁^m+ C₂^m+…+C_r^m=S_k=0^rC_k^m – число слов в любой окрестности.

PS_k=0^rC_k^m<=2^m =>  p<=2^m/S_k=0^rC_k^m

Пример: Кодирования по Хэммингу.

m=3, r=1,   p<=8/C₀³+C₁³=2

a⁽⁰⁾=(0,0,0) |

a⁽¹⁾=(1,1,1) |  d(a⁽⁰⁾, a⁽¹⁾)=3=2k+1

A₀={(0,0,0), (1,0,0), (0,1,0), (0,0,1)}

A₁={(1,1,1), (1,1,0), (0,1,1), (1,0,1)}

(0,1,1)                   (1,1,1)

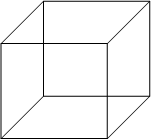  (0,1,0)                   (1,1,0)

(0,0,1)                    (1,0,1)

(0,0,0)                 (1,0,0)

Полиномиальное кодирование.

a=(a₁,a₂, … a_m), a_iÎ{0,1}  | Z₂

Z₂  |  a=(0,1,1,0,1)  x+x²+x⁴

m+k=n₊

g(x)=g₀+g₁x+…+g_kx^k

g₀¹0, g_k¹0

m=5, k=3

a=(0,1,0,1,1)=x+x³+x⁴

g(x)=1+x²+x³

a-g=x+x⁵+x⁷

(0,1,0,0,0,1,0,1)

mx(x+k)