Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 15

   8       9                    

5       6     7

2     3       4

1

8,5,6,7,4,3,2,1

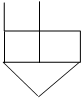
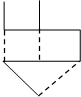
Т – множество ребер, содержащих каркас.

T={(1,2), (2,3), (3,4), (4,7), (7,6), (6,5), (5,8), (6,9)}

Если граф дерево, то существует 1 каркас, если граф цикл, то – несколько.

Следствие к т.51

1) Граф связан G=(V,E)   и есть подмножество ребер FÍE, для любого цикла графа G существует хотя бы 1 ребро не лежащее в F, тогда можно построить каркас Т, все ребра F будут принадлежать T. T=(V,E`) FÍE`

Доказательство:

Мы можем удалить ребро из цикла, не принадлежащее F.

2) Связанный граф с Р вершинами и Р-1 ребрами, является деревом.

Доказательство:

Допустим P, P-1,    если были бы циклы, то при построении Р вершин, было бы Р ребер, т.е. удаляя 1 ребро получим дерево.

3)  Если связанный граф имеет p вершин и q ребер, то q-p+1 >= 0.

Строя каркас, Р и Р-1 ребер, а в графе больше ребер, чем в каркасе. Следовательно это и будет >= 0.

Определение: Есть произвольный граф p – вершин, q – ребер.

k – число компонент связности, тогда говорят, что j:=p-k –называется корангом графа.

m:=q-p+k – называется цикломатическим числом графа.

p₁q₁        p₂q₂     …       p_kq_k

(V₁,E₁)   (V₂,E₂)  …     (V_k,E_k)

k – число компонент связности. Тогда для любой компоненты есть коранг и цикломатическое число.

j_i:=p_i –1       j=S_i=1^kj_i

m_i:=q_i -p_i+1   m=S_i=1^km_i

Теорема: 52

1.  Для любого графа его m>=0, т.к. m_i=q_i-p_i+1>=0  (Теорема 51)

2.  G – связанный

G – дерево <=> m=0 ( необходимый и достаточный признак дерева).

Определение: Пусть есть связанный граф P – вершин, q – ребер

G(V,E),   T=(V,E) – стягивающее дерево

XÎE` - ребра из каркаса называются ветвями, которые не вошли хорды.

Если возьмем каркас и к этому каркасу прибавим хорду, то получим цикл. Этот цикл называется главным циклом, определяемым этой хордой.

yÎE\E`  y – хорда

Каждой хорде соответствует главный цикл.

М – главным циклов (сколько хорд)

P – вершин, q – ребер из них вычесть ветви (p-1)

q-(p-1)=m

Пример: На главные циклы

x_1,x₂,x₃,x₄,x₅ – ветви                  с    ^y1     e    _y2        циклы: bcedb:  y₁

y₁,y₂,y₃ – хорды                        ^x2 b  ^{x3  x4}d_x5     f                   defd :   y₂

a^x1             _y3                             abdfa:   y₃

Определение: Пусть есть каркас данного графа

Элементарное преобразование дерева. Вводим хорду, получаем цикл, удаляем ветвь, получаем каркас.

 

Коциклы

G=(V,E)

Коцикл – минимальное количество ребер при удалении одного из них граф теряет связанность. C=E`ÌE   G`=(V,E\C)

Минимум: Что ни какое собственное подмножество С этим свойством не обладают

{x₁,x₂}  -  коцикл                                                                                    x₃      ^x1

{x₁,x₂,x₃}   -  не является коциклом, т.к. {x₁,x₂} его подмножество              _x2

Определение:  Пусть есть связанный граф G=(V,E)

C – его коцикл

G=(V,E\C)

Получим у G` несколько компонент связности k>=2

Пусть k=3

(V₁,E₁), (V₂,E₂), (V₃,E₃)

т.к. G связан, то существует ребро x, которое соединяет (V₁,E₁) и (V₂,E₂) и оно принадлежит С, тогда если рассмотреть множество С-х  (С\{x}), то все равно граф несвязан, но мы получим множество С-х – коцикл, этого не может быть, т.к. мы предположили, что k=3, a k=2, т.е. при удалении ребер принадлежащих С, граф распадается на 2 компоненты связности.

Ребра коцикла обладают свойством: (они не соединяют V₁ и E₁, V₂ и E₂), они должны соединять V₁ и V₂.

Теорема: 53 При удалении ребра коцикла, он распадается на 2 компоненты связности и ребра коцикла соединяют вершины одной компоненты связности с другой.

Следствие: Любой Цикл и любой коцикл связанного графа имеют четное число общих ребер.

Доказательство:

 

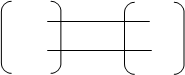(1)        а       (2)

a)  Если цикл принадлежит (1) и  не пересекается с ребром коцикла, четно.

b)  Если цикл пересекается с ребрами, коцикла, то нужно пройти четное число раз, туда и обратно.