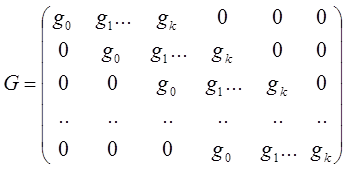Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 8

Правоциркулярная матрица а.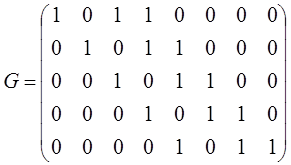

Теорема: 27

Пусть существует многочлен f(x)ÎZ₂ – множество вычетов

(коэффициент из множества Z₂, если он делиться на 1+x, тогда у многочлена четно число не нулевых коэффициентов).

Доказательство:

f(x)=f₀+f_1X+f_2X²+…+f_kX^k

f(x)=(1+x)f₁(x)

f(1)=f₀+f₁+f₂+…+f_n=0  (1+1=0)  => число не нулевых коэффициентов четно.

g(x)=1+x  (m,m+1)

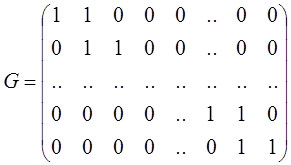
Коды Шеннона-Фено

Свойство префикса – никакая кодовая последовательность не является началом другой кодовой последовательности.

Код – беспрефиксный.

P₁…P_n – вероятность появления какого-либо символа в последовательности.

0<=p<=1

P₁+P₂+…+P_n=1

S₁, S₂, … , S_n – длины кодовых символов.

S_i=1ⁿP_iS_i à min оптимальный код.

Лемма: беспреффиксные коды.

1)  p₁>=p₂>=…>=p_n S₁<=S₂<=…<=S_n

2)  S_n=S_n-1.]  S_n>S_n-1     _______X

S_n-1    - не может быть другим кодом

Алгоритм Хоффмана.

p₁>=p₂>=…>=p_n   Наименьшие встречающиеся слова мы объдиним S₁<=S₂<=…<=S_n

p_n  p_n-1  - 2 редко встречающихся слова

Получаем n-1 слово и т.д. до тех пор пока не останется 2 слова, которым приписывается 0 или 1

Пример:

{a, b, c, d, e} Известны вероятности появления этих слов в тексте.

0,37(a)

0,22(b)

0,16(c)         d,e – самые редко встречающиеся символы, объединем в одно

0,14(d)        Появление символов не зависит друг от друга.

0,11(e)        

Теперь

0,37(a); 0,22(b); 0,16(c); 0,25(de);

Далее:

0,37(a); 0,38(bс); 0,25(de);

0,62(ade); 0,38(bс);

Кодирование 0 и 1

ade           bc

0  1        Присваиваем правому 0, а левому 1

 

a         de   b      c

00       01  10    11           Получается беспреффиксный код

d       e

010    011

Лексикографический порядок

{x₁, x₂,…,x_n}  -  набор каких-либо объектов

{y₁, y₂,…,y_n}  -  x_i, y_iÎX (алфавит)

Можно их сравнить, больше, меньше, равно, не равно

{x₁, x₂,…,x_n}  < {y₁, y₂,…,y_n}  Набор Х в лексикографическом порядке идет                                                    раньше.

Если существует кÎ(1,n) такая, что x_i=y_i для i<k x_k<y_k

Пример: словарь из 3-х символов, тогда в словаре 3-х буквенных слов – 6

{1,2,3}

{1,3,2}

{2,1,3}

{2,3,1}

{3,1,2}

{3,2,1}

Антилексикографический порядок

{x₁, x₂,…,x_n}  < {y₁, y₂,…,y_n}  Набор Х в лексикографическом порядке идет                                                    позже.

Если существует кÎ(1,n) такое, что x_i=y_i для i>k x_k>y_k

Алгоритм лексикографического порядка

n – элементное множество задача перебрать все к – элементные подмножества данного множества. (k<n)

Чтобы их не перепутать (не повторять) будем их перебирать в лексикографическом порядке.

С_n^k – можно выбрать подмножеств из n

{1..k} – первое множество

…

{a₁,a₂,…,a_k}

{a₁,a₂,…,a_p,a_p+1,a_p+2,…,a_p-k+p+1}

p=max{i|a_i<n-k+1}

a[ ] – очередная перестановка

p – переменная которая показывает с какого места мы изменяем

a[i]=i    iÎ[1,k]

p=k

while(p>=1)

{

if(a[k]=n) then p:=p-1

else p:=k;

if (p>=1)

{

a[i]:=a[p]+i-p+1;

for (i=k, k-1, … p)

}

}

Пример n=6  {1,2,3,4,5,6}

k=4

{1,2,3,4}, p=4

{1,2,3,5}, p=4

{1,2,3,6}, p=3

{1,2,4,5}, p=4

{1,2,4,6}, p=3

{1,2,5,6}, p=2

{1,3,4,5}, p=4

{1,3,4,6}, p=3

{1,3,5,6}, p=2

{1,4,5,6}, p=1

{2,3,4,5}, p=4

{2,3,4,6}, p=3

{2,3,5,6}, p=2

{2,4,5,6}, p=1

{3,4,5,6}, выход

15 варинантов

Числа Стирлинга первого и второго рода

S – второго рода;   s (малая) – первого рода

Числа Стирлинга второго рода – S(n,k) – число разбиений n элементного пространства на k  не пересекающихся подмножеств.

S(4,2) = 7  {1,2,3,4}    |             {1,2,3} {4}

{1,2,4} {3}

{1,3,4} {2}

{2,3,4} {1}

{1,2} {3,4}

{1,3} {2,4}

{1,4} {2,3}

Свойства чисел Стирлинга

1)  S(0,0)=1

2)  S(n,k)=0  при k>n

3)  S(n,0)=0

S(n,n)=1

4)  S(n,k)=S(n-1,k-1)+kS(n-1,k)   0<k<n

Доказательство:

Рассмотрим разбиение n множества на k  не пересекающихся подмножеств.

Разбиение: Разобьем на 2 группы: