Ответы на экзаменационные вопросы № 1-51 по дисциплине "Дискретная математика" (Способы представления множеств. Матричное представление графов (ориентированных и неориентированных))

1.Способы представления множеств

Множество–объекты единой природы(элементы различны).

1)  списком своих элементов (перечисление)

2)  порождающей процедурой

3)  описанием характеристических свойств элементов

4)   множества (характреными предикатами)

a)  Графическое

b)  Способ только для конечных множеств

L={a₁,a₂,a₃,…,a₃}

c)  Порождающие процедуры

Индуктивное правило

N – множество натуральных чисел.

N={n=m+1; m принадлежит N₀}

Рекурсивное правило (включает 2 шага)

N={a) 1 принадлежит N; б) если n принадлежит

N, то n+1 принадлежит N

d)  Описание хар-их св-в элементов множества

В случае когда свойство элементов множества М может быть описано коротким выражением (предикатом) Р(х), где предикат обозначает р(х)=’х обладает свойством р’.

М задаётся М={x^p(x)}

x/2 принадлежит N₀

M₂ⁿ={x|x=2^k, k принадлежит N₀}

2.Операции над множествами

1)  Объединением множеств А и В (обозначение - AÈB) называется множество АÈ={x| xÎA или xÎB}.

P_AÈB(x)=P_AvP_B(x)

2)  Пересечением множеств А и В (обозначение - АÇВ) называется множество АÇВ={x| xÎA и xÎB}

P_AÇB(x)=P_A^P_B(x)

3)  Разностью множеств А и В (обозначение - А/В) называется множество А/В={x| xÎA и xÎB}

P_A/B(x)=P_A(x)^¬P_B(x)

4)  Дополнением (до U) множества А называется множество всех элементов, не принадлежащих А (но принадлежащих U).

ùA={x| x Ï A и xÎU}

P_ùA(x)≡ ¬P_A(x)

ùА=U\A. (Множество U должно быть либо задано, либо очевидно из контекста, в противном случае проще пользоваться выражением U\A)

5)   Система множеств, в которой все парные пересечения множеств пусты, называется разбиением множества U всех элементов этих множеств, а множества такой системы называются классами или блоками разбиения.

6)   Симметрическая разность множеств А и В определяется  по формуле AÅB=(A\B) È(B\A)

3)  ассоциативность, коммутативность,

дистрибутивность бинарных операций над

 множествами

Множества относительно операций над множествами образуют булеву алгебру множеств где выполняются основные тождества и законы алгебры:

Коммутативность:

Ассоциативность:

Дистрибутивность:

4)  Запись тождества де-Моргана

 и тождества порецкого

Закон де-Моргана:

Тождество порецкого:

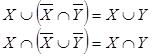
5)  Запись тождества поглощения

и тождества склеивания

Тождество поглощения:

Тождества склеивания:

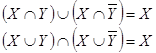
6.конечные множества. мощность множества.

 Множества, состоящие из конечного числа элементов, - конечные. Число элементов в конечном множестве называется мощностью множества М (кардинальное число) и часто обозначается |М|. Множество мощности 0 (не содержащее злементон) называется пустым и обозначается Æ, Принято считать, что пустое множество является подмножеством любого множества.

Обозначения для множеств, принятые в математике:

N - множество натуральных чисел (не включая 0);

Z, Z₊, Z_-- множество целых чисел, множество целых положительных/отрицательных чисел;

Q - множество рациональных дробей вида p/q {p,qÎZ)\

R - Множество действительных чисел;

C - множество комплексных чисел.

9.множество степень.мощность множества степень.

Пусть x,y не пустое мн-во. Y^x мн-во отображения f:xу

Лемма: пусть X Yнепустые конечные  множества, [X]>=2  [Y]>=2, то  [Y^[x]] =[Y]*[Y^x/{x}]

Теорема:  x,y конечные ненулевые мн-ва тогда мощность мн-ва степень [Y^x]= [Y]^[x]

7.булеан множества. построение булеана множества. теорема о числе всех подмножеств конечного множества.

Булеан конечного множества

Множество всех подмножеств конечного множества называется булеаном конечного множества.

Построение булеана

Пусть задано конечное множество V={v₁, v₂. ...v_k}, |V|=k. Для построения булеана β(V) построим вспомогательную таблицу.

Если для конечного множества А мощность равна n, то число всех подмножеств мн-ва А=2ⁿ.

Установленное соответствие м\д мн-вом всех подмножеств А и мн-вом двоичн.векторов длинны n явл взаимооднозначным соответствием.

Число подмн-в мн-ва А или мощ-ть булиана кнечного мн-ва А равна мощности мн-ва В_n. Мн-во двоичных векторов – это мн-во буля взятого n-раз.

B_n=В*В*В*…*В*В={0,1}-мн-во буля

B_n={0,1}*{0,1}*{0,1}*…*{0,1}={(b₁,b₂,…,b_n)\b_iÎB; i=1,n}

[B]ⁿ=2ⁿ = [B_n]

Мн-ва равномощны если м\д их эл-тами можно установить ВОЗ.

8.Прямоепроизведениемножеств. теорема о мощности множества, которое есть прямое произведение множеств.

Прямым произведением множеств А и В (А*В) называется множество всех пар вида (а,b), таких, что аÎА, bÎВ (А*В ={(а,b) | aÎА, bÎВ}).Прямым произведением множеств А₁,...,А_n (A₁*…*A_n) называется множество всех векторов (а_1,...,а_n)

длины n, таких, что а₁ÎА,..., a_nÎА_n (А₁*...*А_n={(а₁,…, а_n) | a₁ÎА₁,…а_nÎА_n}).

Теорема 1. Пусть А₁,...,A_n - конечные множества и |А₁|=m₁,…, |А_n|=m_n. Тогда мощность множества А₁*...*А_n равна произведению мощностей А₁,.... А_n:|А₁*...*А_n| = m₁…m_n.

Вектор – упорядоч. Набор эл-ов. а=(а₁ а₂ …а_n). Число координат вектора наз.его размерностью.

2 вектора равны если равны их размерности.

Док-во теоремы проводим методом мат.индукции.

1)n=1 [A₁]=m₁ – теорема верна.

2)индуктивность предположения предполаг.,что теорема верна при n=k

3)верна и для  n=k+1

29. ассоциативность, коммутативность, дистрибутивность.

Операция называется ассоциативной, если для любых элементов а, b, с (aμb)μс=aμ (bμс).

Операция μ называется коммутативной, если для любых элементов а, b aμb=bμa

Операция μ называется дистрибутивной слева относительно операции Ψ, если для любых а, b, с аμ(bΨс)=(aμb) Ψ (aμc), и дистрибутивной справа относительно Ψ, если (аΨb)μс=(aμc) Ψ (bμc)

10.Теорема Кантора. Парадокс Кантора.

В теории множеств теорема Кантора гласит, что:

Любое множество менее мощно, чем множество всех его подмножеств

Парадо́кс Ка́нтора — парадокс теории множеств, который демонстрирует, что предположение о существовании множества всех множеств ведёт к противоречиям и, следовательно, противоречивой является теория, в которой построение такого множества возможно.

Формулировка:

Предположим, что множество всех множеств

существует. В этом случае справедливо , то есть всякое множество t является подмножеством V.

Но из этого следует  — мощность любого множества не превосходит мощности V.

11.теоремы о счётных множествах.

Мн-во равномощное мн-ву N наз. счетным. [E]=X₀  например Установим ВОЗ м\д {(n;2^n-1),nÎN}

Любое бесконечн.подмн-во мн-ва N счетно.

Теоремы:

1)Всякое беконечн.мн-во содержит счетное подмн-во.

2)Всякое бесконечн.подмн-во счетного мн-ва, счетно.

3)Мн-во всех целых чисел Ζ счетно.

4)Обьединение счетного мн-ва А и конечного мн-ва В – счетно.

5) Обьединение конечного мн-ва счетных мн-в, счетно.

6) Обьединение счетного мн-ва счетных мн-в счетно.

7) декартово произведение счетных множеств счетно.

8)мн-во всех рацион.чисел счетно.

9) мн-во всех алгебраичн.чисел счетно.

Мощность несчетного мн-ва есть континиум.

10) мощ-ть булиана бесконечн.счетного мн-ва Е превышает мощ-ть мн-ва Е

11) мощ-ть булиана бесконечного счетного мн-ва Е бессчетно и его мощ-ть равна континиуму.

12.что называется соответствием.область определения и значения соответсвия.полность определенное и сюръективное соответсвие.

Соответствием между множествами А и В называется подмножество GÍА*В.

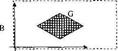Если (a,b)ÎG, то говорят, что b соответствует а при соответствии G.Областью определения соответствия называется множество пp1G (проекция соответствия на первую ось), множество пp2G (проекция соответствия на вторую ось) - областью значений соответствия.Если пp1G= А, то соответствие называется всюду определенным (полностью определенным), в противном случае соответствие называется частичньм.Если пp2G =В, соответствие называется сюръективным.Множество всех bÎВ, соответствующих элемент аÎА, называется образом а в В при соответствии G. Множество всех а, которым соответствует b, называется прообразом b в А при соответствии G.

13.функциональное соответствие.

Соответствие G Í AxB называется функциональным (или однозначным