Расчетно-графические работы по дисциплине "Дискретная математика": Учебно-методическое пособие

5. ТАБЛИЦА  ИСТИННОСТЕЙ  ЛОГИЧЕСКИХ  ФУНКЦИЙ  ДВУХ  ПЕРЕМЕННЫХ

x1  x2

y0

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

y12

y13

y14

y15

0  0 0  1 1  0 1  1

0 0 0 0

0 0 0 1

0 0 1 0

0 0 1 1

0 1 0 0

0 1 0 1

0 1 1 0

0 1 1 1

1 0 0 0

1 0 0 1

1 0 1 0

1 0 1 1

1 1 0 0

1 1 0 1

1 1 1 0

1 1 1 1

Символ операции

0

Ù × &

x1

x2

Å

Ú +

¯

~

Øx2

Øx1

®

|

1

6. ПРИМЕР  РЕШЕНИЯ  ВАРИАНТА РАСЧЕТНО-ГРАФИЧЕСКОЙ  РАБОТЫ №2

АЛГЕБРА  ЛОГИКИ

1.  Построить таблицу истинности логической функции

f(x,y,z)= (Øz®y) Å ((y®x)&z);

для заданной функции f построить логическую схему.

Решение

Таблица истинности для функции f(x,y,z)= (Øz®y) Å ((y®x)&z):

x, y, z	Øz	(Øz®y)	(y®x)	&z	Å
0 0 0	1	0	1	0	0
0 0 1	0	1	1	1	0
0 1 0	1	1	0	0	1
0 1 1	0	1	0	0	1
1 0 0	1	0	1	0	0
1 0 1	0	1	1	1	0
1 1 0	1	1	1	0	1
1 1 1	0	1	1	1	0

Логическую схему можно построить по СДНФ функции:

f(x,y,z) = ØxyØzÚ Øxyz ÚxyØz

 

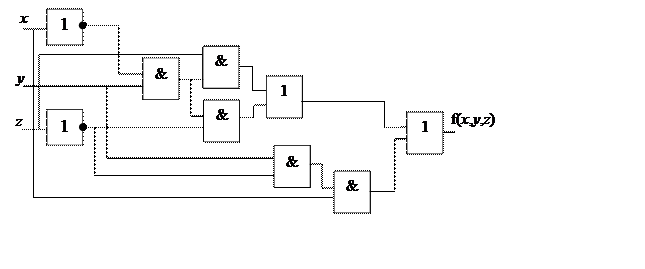СДНФ можно минимизировать, тогда логическая схема упроститься, аналогично строится схема и для упрощенной формы.

 

2.  Логическую функцию Z(A,B) = ØAÚB & AÚB & ØA представить картой Вейча.

Решение

Этот вопрос дается на самостоятельное рассмотрение, поэтому, для функции трех переменных построить карту Вейча, используя рекомендованную литературу.

Для заданной функции Z(A,B) карта Вейча имеет вид:

1	1
0	1

3.  Функцию g(x,y)=1 представить в базисе {Ú,Ø}.

Решение

Запишем сначала СДНФ функции g(x,y)=1, а затем исключим из формулы все конъюнкции, используя тождество де-Моргана:

g(x,y)= ØxØyÚxØyÚØxyÚxy=Ø(xÚy)ÚØ(xÚØy)ÚØ(ØxÚy)ÚØ(ØxÚØy)=1.

4.  Для функции f(x,y,z,t) = Øxyt Ú xyØz Ú xØzt Ú xzØt получить ее СДНФ и СКНФ:

a) по таблице истинности;

b) используя законы 0 и 1;

c) минимизировать СДНФ методом Блейка-Порецкого.

5.  Проверить равносильность формул f1 и f2:

f1=xÚ(y &Øz) ® (Øx®y);

f2= ØyÚz.

Решение

Проверим равносильность на наборах, при этом надо учитывать, что функция f2 есть функция от двух переменных, а функция f1 – функция от трех переменных, поэтому в функцию f2 введем фиктивную переменную, получим выражение для f2= (x&Øx)Ú(ØyÚz):

x, y, z	xÚ(y &Øz)	(Øx®y)	f1	0Ú(ØyÚz)	f2
0 0 0	0	0	1	1	1
0 0 1	0	0	1	1	1
0 1 0	1	1	1	0	0
0 1 1	0	1	1	1	1
1 0 0	1	1	1	1	1
1 0 1	1	1	1	1	1
1 1 0	1	1	1	0	0
1 1 1	1	1	1	1	1

Формулы f1 и f2 неравносильны, т.к. их значения совпадают не на всех наборах переменных.

ЛОГИКА  ПРЕДИКАТОВ

6.  Предикат P(x,y) задан таблицей на предметной области D={a,b,c}, провести квантификацию и определить логический смысл формул:

1) $x$y P(x,y);

2) "xP(x,c);

3) $yP(b,y).

x  y	P(x,y)
a   a	0
a   b	1
a   c	0
b   a	0
b   b	1
b   c	1
c   a	1
c   b	0
c   c	0

Решение

1)  $x$y P(x,y) – значение предикатной формулы равно истина, т.к. существуют и x и y, такие что предикат Р принимает значение истина;

2)  "xP(x,c) – значение предикатной формулы равно ложь, т.к. не для каждого x при y=c предикат Р принимает значение истина;

3)  $yP(b,y) значение предикатной формулы равно истина, т.к. существует такой y, (например y=b), что предикат Р принимает значение истина.

7.  Проверить истинность, ложность или выполнимость предикатной формулы, на множестве N₀:

($x)(å(x,y,y)®("y)å(x,y,y)).

Решение

Предикатная формула тождественно истинна.

Высказывание, выраженное формулой следующее: «Если существует x, такой что x+y=y, то для любого y выполняется x+y=y».

          Рассмотрим левую и правую часть импликации.

На множестве натуральных чисел с нулевым элементом N₀ существует такое число x=0, что x+y=y, таким образом левая часть импликации истинна на N₀. Если предикатная формула находится в области действия квантора по переменной x, то при x=0 для любого y будет выполняться x+y=y. Следовательно, импликация, в которой левая и правая часть истинна –  истинна, формула тождественно истинна на множестве N₀.

7. ВАРИАНТЫ  РАСЧЕТНО-ГРАФИЧЕСКОЙ  РАБОТЫ №2

АЛГЕБРА  ЛОГИКИ

Вариант 1

1.  Построить таблицу истинности логической функции

f(x,y,z) = Ø(x&(z®y))Ú ((y®Øx)&z);

для заданной функции f построить логическую схему.

2.  Логическую функцию Z(A,B,C) = AÚBÚØB&C представить картой Вейча.

3.  Функцию g(x,y)=xÅy  представить в базисе {&,Ú,Ø}.

4.  Для функции f(x,y,z,t) = ØxyÚyØzÚØztÚxØt получить ее СДНФ и СКНФ:

a) по таблице истинности;

b) используя законы 0 и 1;

c) минимизировать СДНФ методом Блейка-Порецкого.

5.  Проверить законы поглощения и склеивания с помощью эквивалентных преобразований выражений.

ЛОГИКА  ПРЕДИКАТОВ

6.  Предикат P(x,y) задан таблицей на предметной области D={a,b,c}, провести квантификацию и определить логический смысл формул:

1) "x"yP(x,y);  2) $xP(x,a); 3) "yP(b,y).

x  y	P(x,y)
a   a	1
a   b	1
a   c	1
b   a	1
b   b	0
b   c	1
c   a	1
c   b	1
c   c	1

АЛГЕБРА  ЛОГИКИ

Вариант 2

1.  Построить таблицу истинности логической функции

f(x,y,z) = (x&z®y)ÅØ (yÚx®Øx&z);

для заданной функции f построить логическую схему.

2.  Логическую функцию Z(A,B,C)=ABØCÚØABCÚAØBØCÚABC представить картой Вейча

3.  Функцию g(x1, x2)= x1 Å x2 представить в базисе {Ø,Ú}.

4.  Для функции f(x,y,z,t) = xyzÚyztÚxzt получить ее СДНФ и СКНФ:

a) по таблице истинности;

b) используя законы 0 и 1;

c) минимизировать СДНФ методом Блейка-Порецкого.

5.  Путешественник попал к людоедам. Они разрешают ему произнести какое-нибудь высказывание  и ставят условие, что если его высказывание будет истинным, то его сварят, а если ложным, то зажарят. Какое высказывание следует произнести путешественнику, чтобы избежать гибели?

ЛОГИКА  ПРЕДИКАТОВ

6.  Предикат P(x,y) задан таблицей на предметной области D={a,b,c}, провести квантификацию и определить логический смысл формул:

1) $x$yP(x,y);  2) $xP(x,a); 3) "yP(a,y).

x  y	P(x,y)
a   a	0
a   b	0
a   c	0
b   a	1
b   b	0
b   c	1
c   a	0
c   b	0
c   c	0

АЛГЕБРА  ЛОГИКИ

Вариант 3

1.  Построить таблицу истинности логической функции

f(x,y,z) = (x&y&z®Øy)~Ø(x&z®yÚx);

для заданной функции f построить логическую схему.

2.  Логическую функцию Z(A,B,C)=ØAØBCÚØABCÚAØBCÚAØBC представить картой Вейча

3.  Функцию g(x,y)= Øy Å Øx представить в базисе {Ø,&}.

4.  Для функции f(x,y,z,t) = xØyztÚxØyzÚØztÚØxt получить ее СДНФ и СКНФ:

a) по таблице истинности;

b) используя законы 0 и 1;

c) минимизировать СДНФ методом Блейка-Порецкого.

5.  Проверить законы поглощения и склеивания с помощью таблиц истинности