Сигналы в радиотехнических системах. Сложные сигналы в радиотехнических системах. Обнаружение радиосигналов. Различение радиосигналов

1.  Сигналы в РТС

1.1. Краткие теоретические сведения

Сигналы, как переносчики информации, представляют собой гармонические колебания, частота, фаза, временная задержка, длительность, амплитуда, которых может изменяться по закону передаваемой или извлекаемой информации. От выбора формы сигнала, вида информационной модуляции зависят такие показатели качества радиотехнической системы (РТС), как помехоустойчивость, точность (достоверность), разрешающая способность, информационная защищенность и др. Сигналы характеризуются длительностью Т₀, временем анализа, эффективной полосой частот (F_ЭФ), энергией (Е₀), мощностью (Р₀), видом информационной модуляции, корреляционной функцией, базой. Время анализа сигналов, передающих непрерывные сообщения, зависит от верхней граничной частоты сообщения (F_В) и, в соответствии с теоремой Котельникова не превышает величины 1/2F_В .

Эффективная полоса частот, занимаемая сигналом определяется выражением:

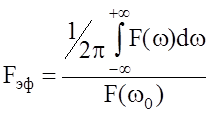,                                                                (1)

где 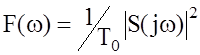 – спектральная плотность сигнала,  – спектральная функция сигнала,  – мощность на несущей частоте сигнала. Для видео сигнала .

Спектральная функция сигнала  находится из прямого преобразования Фурье:

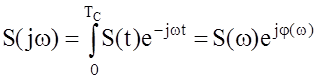,                                              (2)

а .

Энергия сигнала определяется как:

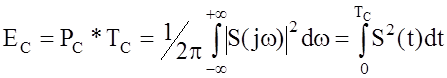 .                                    (3)

Если передаваемое сообщение , то для амплитудной (АМ), фазовой (ФМ) и частотной (ЧМ) видов модуляции имеем:

,

,

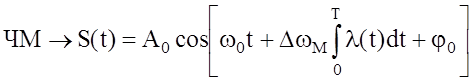.                                 (4)

В (4) М – коэффициент амплитудной модуляции,  – приращение фазы,  – девиация частоты. Величины  и 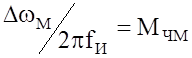 соответственно индексы фазовой и частотной модуляции, а  – полоса частот сообщения . Чем больше отличаются индексы модуляции от единицы, тем больше в спектр информационных составляющих и шире спектр сигнала. Отсюда и высокая потенциальная помехоустойчивость у сигналов с угловой модуляцией (ФМ и ЧМ) по сравнению с АМ.

, , .                    (5)

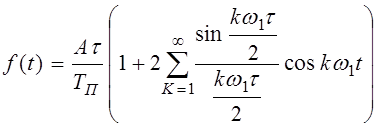Насыщены информационными составляющими сигналы с импульсными видами модуляции (АИМ, ШИМ, ФИМ, КИМ). При разложении периодической импульсной последовательности с амплитудой А, длительностью импульса  и периодом следования  в ряд Фурье имеем: ,                                                        (6)

где для

АИМ , , ;

ШИМ , , ;

ЧИМ , , .

Следует отметить, что эффективная полоса частот занимаемая сигналом (6), практически не зависит от вида модуляции и определяется лишь минимальной длительностью импульса и его формой.

Важной характеристикой сигнала является корреляционная функция. Для ансамбля сигналов , i=1,2,…,m,  это автокорреляционная (АКФ) каждого сигнала и функция взаимной корреляции (ФВК) между любой парой сигналов ансамбля.

АКФ сигнала :

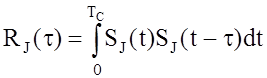.                                                       (7)

Основные свойства АКФ:

а) , б)  – энергия сигнала, в) , г) .

Для сигналов с одинаковой энергией Е применяют нормированную АКФ:

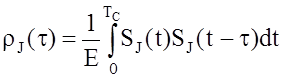.                                                              (8)

В соответствии с преобразованием Винера-Хинчина:

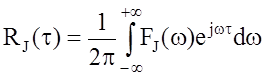.                                                                   (9)

При корреляционном анализе дискретных и цифровых сигналов применяют решетчатую АКФ:

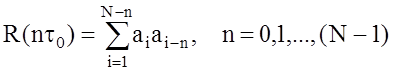,                        (10)

где  – символы дискретной или цифровой последовательности длительности ; N – значность (количество символов) дискретного (цифрового) сигнала на длительность .

Если сигналы периодические, то по (7),(8),(9) можно вычислить АКФ периодического сигнала, считая временные сдвиги, как циклические.

Решетчатая АКФ периодического сигнала записывается так:

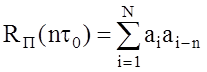.                                                                                     (11)

ФВК сигналов ансамбля:

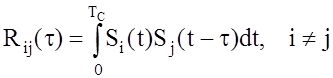.                                                                (12)

Нормированная запись ФВК для сигналов с одинаковой энергией Е:

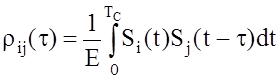.                                                                        (13)

Основные свойства ФВК:

а) ;

б) ;

в)  – коэффициент взаимной корреляции,  ;

г)  - взаимно ортогональны;

д) ,

е) если ,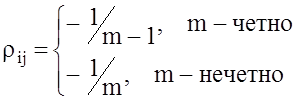

то система сигналов  называется симплексной (равноудаленной).

Обобщенной функцией, устанавливающей связь между элементами сигнала во временной и частотной областях, является двумерная корреляционная функция:

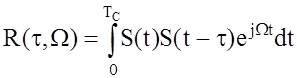.                                                                      (14)

Модуль нормированной двумерной корреляционной функции называется функцией неопределенности (ФН) сигнала:

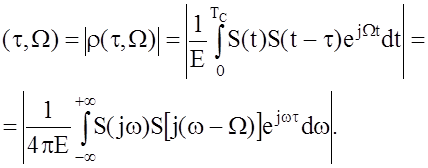                                          (15)

Основные свойства ФН:

a)  ,

b)  ,

c) 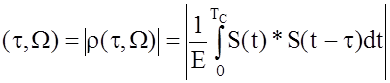  – есть модуль нормированной АКФ.

d) 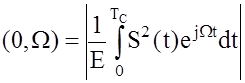  – есть модуль спектральной функции квадрата огибающей сигнала.

e) 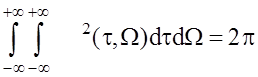  – объем, ограниченный ФН, есть величина постоянная, не зависящая от формы сигнала.

f)  Сечение ФН горизонтальной плоскостью на уровне 0,5 называется диаграммой неопределенности (ДН).

По виду ДН  можно произвести оценку потенциальной точности, разрешающей способности и однозначности при измерении временной задержки и смещения частоты сигнала. Ширина ДН по  и  определяется интервалами неопределенности.

1.2 Примеры.

1.2.1. Определить , занимаемую огибающей прямоугольного радиоимпульса длительности .