Для
построения диаграммы неопределённости необходимо знать девиацию частоты ЛЧМ
сигнала – ![]() и интервал неопределенности по частоте –
и интервал неопределенности по частоте – ![]() .
.
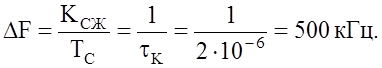
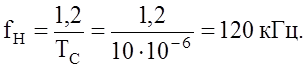
ДН имеет вид:
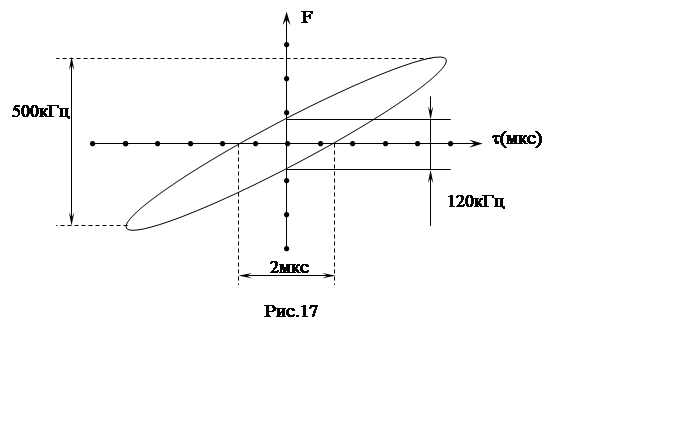 |
2.2.2. Сформировать М-последовательность значимости ![]() . Убедиться в свойствах 2-5. Вычислить АКФ
последовательности. Доказать, что М-последовательность, сформированная вторым
полиномом (дополняющим первый), имеет обратный порядок следования символов.
. Убедиться в свойствах 2-5. Вычислить АКФ
последовательности. Доказать, что М-последовательность, сформированная вторым
полиномом (дополняющим первый), имеет обратный порядок следования символов.
Порядок последовательности: ![]() ,
откуда
,
откуда ![]() . Общая запись генераторного полинома:
. Общая запись генераторного полинома: ![]() .
.
Так
как количество коэффициентов ![]() должно быть четным, то
только два полинома удовлетворяют этому требованию:
должно быть четным, то
только два полинома удовлетворяют этому требованию:
![]()
![]()
Рекуррентная формула генерирования по первому полиному имеет вид:
![]() .
.
Следовательно, М-последовательность формируется на основе 3-разрядного регистра сдвига с двумя выходами в цепи обратной связи.
Сформируем М-последовательность для начальной комбинации в регистре сдвига 111:
|
|
1 |
1 |
1 |
|||
|
1 такт |
0 |
1 |
1 |
1 |
||
|
2 такт |
1 |
0 |
1 |
1 |
||
|
3 такт |
0 |
1 |
0 |
1 |
||
|
0 |
0 |
1 |
0 |
||
|
5 такт |
1 |
0 |
0 |
1 |
||
|
6 такт |
1 |
1 |
0 |
0 |
||
|
7 такт |
1 |
1 |
1 |
0 |
Таким образом, с выхода регистра сдвига сформирована последовательность 1110100, у которой количество "1" на единицу больше количества "0" и присутствуют все трёхзначные комбинации, кроме 000. Сложим по модулю 2 полученную последовательность с её циклическим сдвигом вправо на 1 символ:
|
|
1 |
1 |
0 |
1 |
0 |
0 |
||
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
||
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Полученная последовательность 1001110 отличается от первоначальной циклическим сдвигом на 4 символа.
 Вычислим АКФ последовательности:
Вычислим АКФ последовательности:
|
+ |
+ |
+ |
– |
+ |
– |
– |
|
|
– |
– |
– |
– |
+ |
– |
+ |
+ |
|
– |
– |
– |
– |
+ |
– |
+ |
|
|
+ |
+ |
+ |
+ |
– |
+ |
||
|
– |
– |
– |
– |
+ |
|||
|
+ |
+ |
+ |
+ |
||||
|
+ |
+ |
+ |
|||||
|
+ |
+ |
||||||
|
-1 |
-2 |
-1 |
0 |
1 |
0 |
7 |
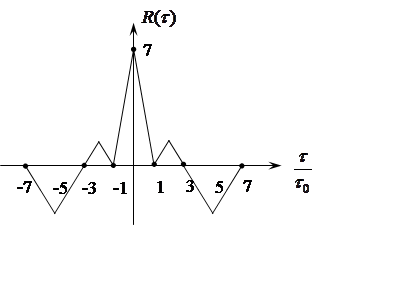
На рис 19 приведен график АКФ одиночной М-последовательности, сформированной по первому полиному с начальной комбинацией 111. Сформируем М-последовательность по второму полиному:
![]()
возьмём начальную комбинацию 100, тогда сформированная последовательность имеет вид 0010111, которая отличается от первоначальной порядком следования символов.
|
0 такт |
1 |
0 |
0 |
|
|
1 такт |
0 |
0 |
0 |
0 |
|
2 такт |
1 |
0 |
1 |
0 |
|
3 такт |
1 |
1 |
0 |
1 |
|
4 такт |
1 |
1 |
1 |
0 |
|
5 такт |
0 |
1 |
1 |
1 |
|
6 такт |
0 |
0 |
1 |
1 |
|
7 такт |
1 |
0 |
0 |
1 |
2.2.3. Сформировать ЧКП ![]() .
Какова связь между этими последовательностями? Вычислить их АКФ. Определить
коэффициенты корреляции между ними. Формирование будем вести по двоичному
представлению номера последовательности в соответствии со свойством 2.
.
Какова связь между этими последовательностями? Вычислить их АКФ. Определить
коэффициенты корреляции между ними. Формирование будем вести по двоичному
представлению номера последовательности в соответствии со свойством 2.
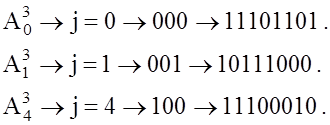
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.