4. При суммировании по модулю 2 любой М-последовательности с ее циклическим сдвигом меньше периода получается та же М-последовательность, но с другим циклическим сдвигом.
5. Количество М-последовательностей одной значности определяется выражением:
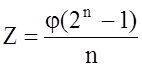 , (21)
, (21)
где ![]() – функция Эйлера, равная
количеству целых положительных чисел, включая единицу, меньших Х и взаимно
простых с Х . Причем если Х – простое число, то
– функция Эйлера, равная
количеству целых положительных чисел, включая единицу, меньших Х и взаимно
простых с Х . Причем если Х – простое число, то ![]() .
.
Таблицы порождающих полиномов М-последовательностей приведены в (3).
6. АКФ одиночной М-последовательности в общем виде записывается в следующем виде:
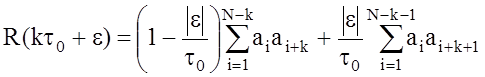 , (22)
, (22)
где ![]()
Граничные значения нормированной АКФ:
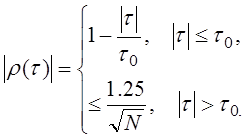 (23)
(23)
7. Нормированная АКФ периодической М-последовательности в пределах одного периода описывается выражением:
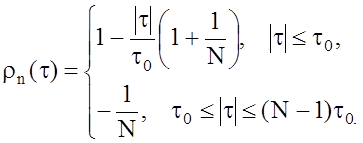 (24)
(24)
8. Энергетический спектр одиночной М-последовательности определяется выражением:
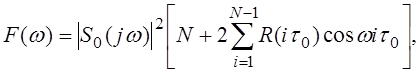 где
где 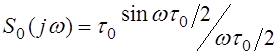 - спектральная функция
единичного импульса длительности
- спектральная функция
единичного импульса длительности ![]() ,
,
![]() решетчатая АКФ
М-последовательности.
решетчатая АКФ
М-последовательности.
Выражение для энергетического спектра периодической М-последовательности имеет вод
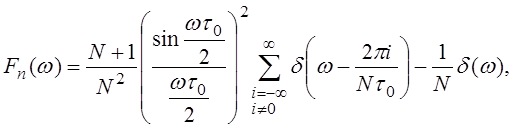 (25)
(25)
где ![]() - дельта-функция.
- дельта-функция.
Спектр имеет линейчатый характер, а мощность i-й гармоники (исключая i=0) равна:
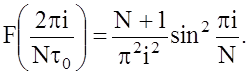
Основные свойства ЧКП
1. Класс нелинейных последовательностей значности ![]() , описываемый выражением:
, описываемый выражением:
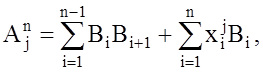 (26)
(26)
где ![]() - запись одиночной ЧКП
длительности
- запись одиночной ЧКП
длительности ![]() порядка n номера j, символы которой
порядка n номера j, символы которой ![]() –
функция Радемахера, определяема на длительности с номером i.
–
функция Радемахера, определяема на длительности с номером i.
![]() –
значение i–го разряда номера последовательности j,
представленного в n–разрядном двоичном виде. Суммирование осуществляется
по модулю 2, а умножение – логическое.
–
значение i–го разряда номера последовательности j,
представленного в n–разрядном двоичном виде. Суммирование осуществляется
по модулю 2, а умножение – логическое.
2. Количество одной значности Z=N, и каждой из них в семействе присваивается номер от 0 до N-1. По n-разрядному двоичному номеру ЧКП формируется последовательность по следующему алгоритму:
если первый разряд двоичного номера – «0», то записываются два символа 11;
если первый разряд двоичного номера – «1», то записываются два символа 10;
для всех последующих разрядов двоичного номера, начиная со второго, нулю соответствует приписывание к исходной комбинации такой же по размеру комбинации, но отличающейся от исходной инвертированной второй половиной; а единице – инвертирование первой половины приписываемой комбинации.
3. Разность ![]() между количеством
разных символов в ЧКП зависит от порядка n и определяется
соотношением:
между количеством
разных символов в ЧКП зависит от порядка n и определяется
соотношением:
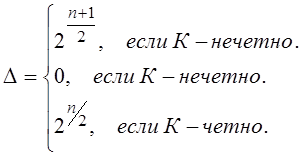
![]() соответствуют
последовательности, в двоичных номерах которых на нечетных позициях имеется
нечетное количество «1».
соответствуют
последовательности, в двоичных номерах которых на нечетных позициях имеется
нечетное количество «1».
4. Каждой ЧКП ![]() соответствует
парная
соответствует
парная ![]() , причем
, причем ![]() . У
парных последовательностей первые
. У
парных последовательностей первые ![]() символа совпадают, а
последующие
символа совпадают, а
последующие ![]() – противоположны (или наоборот).
– противоположны (или наоборот).
5. Каждой ЧКП ![]() соответствует
смежная
соответствует
смежная ![]() , причем
, причем ![]() . У
смежных последовательностей символы, стоящие на нечетных позициях, совпадают и
не совпадают символы, стоящие на четных позициях (или наоборот).
. У
смежных последовательностей символы, стоящие на нечетных позициях, совпадают и
не совпадают символы, стоящие на четных позициях (или наоборот).
6. Любая ЧКП значности N получается из двух парных последовательностей значности N/2 путем их присоединения или из двух смежных той же значности (N/2) путем чередования их символов.
7. Граничные значения нормированной АКФ одиночной ЧКП определяются соотношением
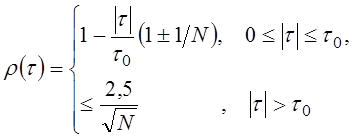 (27)
(27)
Причем решетчатая АКФ при четных сдвигах принимает нулевые значения.
8. Граничные значения нормированной АКФ периодической ЧКП в пределах одного периода определяются соотношением
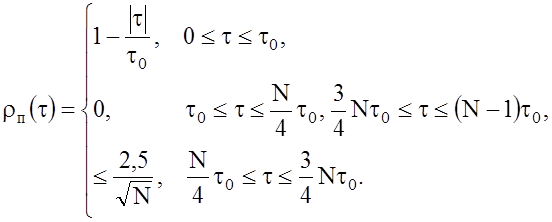
9. АКФ парных и смежных ЧКП имеют боковые остатки при одинаковых сдвигах, равные по абсолютной величине и противоположные по знаку:
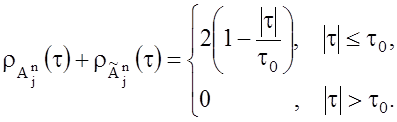
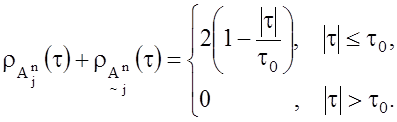
Это свойство характерно для дополнительных последовательностей (серий), описанных Голеем [4]. Все свойства присущие дополнительным последовательностям, справедливы и для семейства ЧКП.
10. Все ЧКП одной значимости взаимно ортогональны.
11. Описание энергетического спектра одиночной ЧКП ничем не отличается от аналогичного описания М-последовательности. Энергетический спектр периодической ЧКП описывается выражением
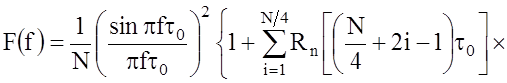 (29)
(29) 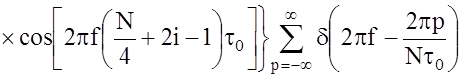
2.2. Примеры
2.2.1.
Длительность ЛЧМ сигнала ![]() =10мкс, его время
корреляции
=10мкс, его время
корреляции ![]() =2мкс. Определить коэффициент сжатия –
=2мкс. Определить коэффициент сжатия – ![]() . Нарисовать диаграмму неопределённости
сигнала.
. Нарисовать диаграмму неопределённости
сигнала.
По
определению 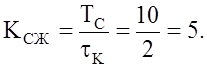
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.