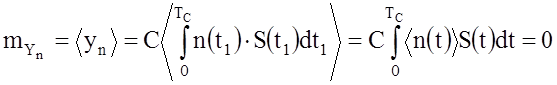Сигналы в радиотехнических системах. Сложные сигналы в радиотехнических системах. Обнаружение радиосигналов. Различение радиосигналов, страница 8

,

;                          (31)

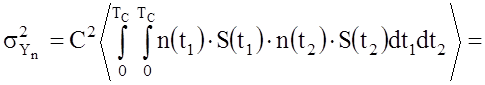
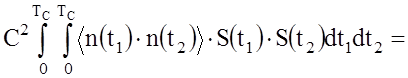
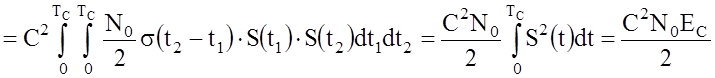   (32)

          Отношение сигнал /шум по мощности на выходе КР в момент  равно

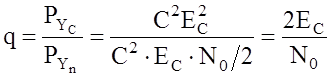                                                                 (33)

и дает потенциальную оценку помехоустойчивости коррелятора, если обеспечивается синхронизирующего устройства (СУ) синхронизация  по временному положению сигналов  и .

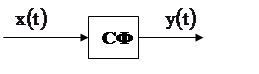          Согласованный фильтр (рис. 22) как оптимальный линейный фильтр для сигнала

Рис. 22

характеризуется коэффициентом передачи  или импульсным откликом :

,         ,

                                                                                   (34)

функция комплексно-сопряженная со спектральной функцией сигнала .

Функция  на выходе СФ определяется как свёртка между входным процессом  и импульсным откликом :

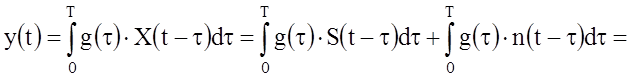
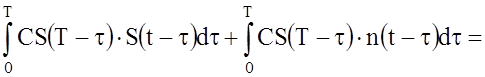
.                               (35)

Полезная составляющая  на выходе СФ с точностью до постоянного коэффициента С является АКФ сигнала  и в момент времени  принимает максимальное значение

АКФ шумового компонента :

.

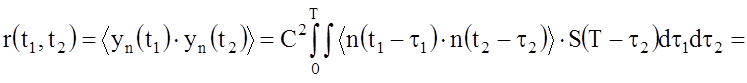
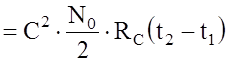При                   и

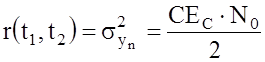
Следовательно, отношение сигнал/шум на выходе СФ для пикового значения полезного сигнала такое же, как и для коррелятора, т.е. 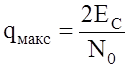. Если шум  не белый, а произвольный гауссов со спектральной плотностью , то

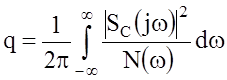                                                              (37)

3.2. Примеры.

3.2.1. На вход КР и СФ поступает прямоугольный видеоимпульс с параметрами

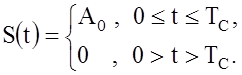
 имеют следующие характеристики:  ;

.

Изобразить функцию у(t) на выходе . Описать параметры выходных сигналов.

Из условия задачи вытекает x(t)=S(t), поэтому на выходе К_Р будем наблюдать процесс накопления в пределах времени Т_С (рис. 23б), а на выходе С_Ф – вычисление АКФ сигнала S(t) (рис. 23в).

Для коррелятора:

 

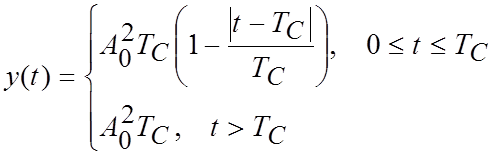
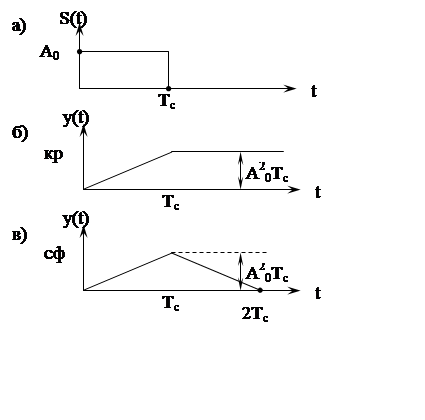
Рис. 23

Для согласованного фильтра:

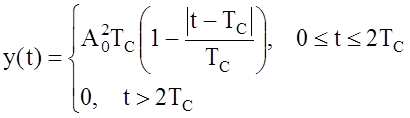
3.2.2 На вход  поступает сложный сигнал вида:

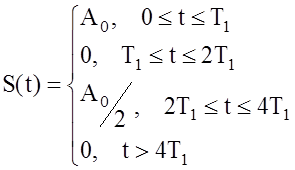
 имеют следующие характеристики: ;

. Изобразить функции y(t) на выходе . Описать параметры выходных сигналов.

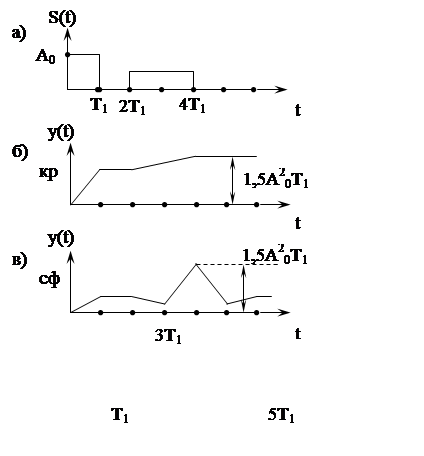
Как и в предыдущей задаче, для К_Р – накопление квадрата функции, для С_Ф – вычисление АКФ (рис. 24).

Для коррелятора:

 

Рис. 24

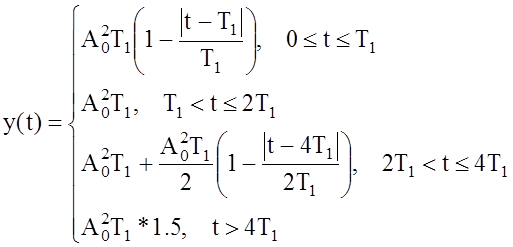
Для согласованного фильтра:

, т.е. АКФ сигнала S(t), которую можно вычислить через решетчатую функцию (рис. 24):

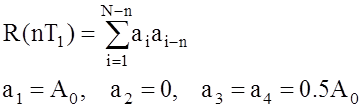
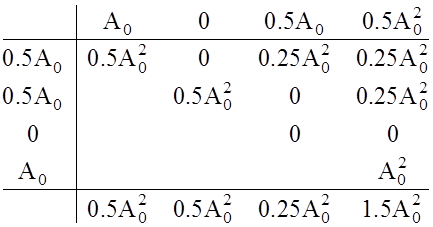
Отсюда:

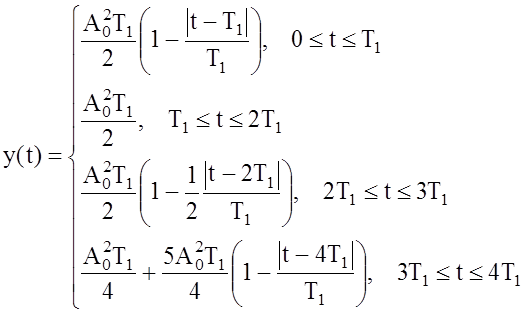
3.3 Задачи

3.3.1. На вход  поступает сигнал . Импульсный отклик фильтра . Нарисовать форму сигнала на выходе , если  – М-последовательность с генераторным полиномом  и начальной комбинацией – все единицы. Символы последовательности принимают значения .

3.3.2. На вход  поступает сигнал . Опорный сигнал коррелятора . Нарисовать форму сигнала на выходе , если  – М-последовательность с генераторным полиномом  ,  – М-последовательность с генераторным полиномом , начальные комбинации сигналов  и  одинаковые. Символы М-последовательностей принимают значения .

3.3.3. На вход  поступает сигнал . Импульсный отклик фильтра ,  – сигнал, наблюдаемый на интервале . Нарисовать форму сигнала на выходе , если  – М-последовательность с генераторным полиномом  ,  – М-последовательность с генераторным полиномом , начальные комбинации сигналов  и  одинаковые. Символы М-последовательностей принимают значения .

3.3.4. На вход  поступает смесь +, . Импульсный отклик фильтра . Нарисовать форму сигнала на выходе , если  и  – четверично-кодированные видеопоследовательность соответственно  и  . Символы видеопоследовательностей принимают значения .

3.3.5. На вход  поступает смесь +, . Опорный сигнал коррелятора . Нарисовать форму сигнала на выходе , если  и  – четверично-кодированные видеопоследовательность соответственно  и  . Символы видеопоследовательностей принимают значения .

3.3.6. На вход  поступает смесь +, . Опорный сигнал коррелятора . Нарисовать форму сигнала на выходе , если ,  и – четверично-кодированные видеопоследовательность соответственно ,  и . Символы видеопоследовательностей принимают значения .

На вход  поступает смесь +, . Импульсный отклик фильтра ,  – сигнал, наблюдаемый на интервале . Нарисовать форму сигнала на выходе , если ,  и – четверично-кодированные видеопоследовательность соответственно ,  и . Символы видеопоследовательностей принимают значения .

Обнаружение радиосигналов.