Сигналы в радиотехнических системах. Сложные сигналы в радиотехнических системах. Обнаружение радиосигналов. Различение радиосигналов, страница 4

Все сложные сигналы с помощью специальных устройств можно сжать по длительности. Коэффициент сжатия определяется базой сигнала. В современных РТС нашли применение детерминированные сложные сигналы как с непрерывной модуляцией, так и с дискретной.

Среди сигналов с непрерывной модуляцией наибольшее распространение получили сигналы с линейной частотной модуляцией (ЛЧМ – сигналы). Из сложных сигналов с дискретными видами модуляции уделяется внимание псевдослучайным сигналам с дискретными фазовой и частотной модуляциями.

У ЛЧМ сигналов расширение спектров осуществляется за счет девиации частоты по линейному закону в пределах длительности сигнала.

Если описание ЛЧМ сигнала представить в следующей форме:

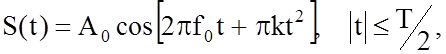
то  – центральная частота,  – закон изменения частоты,  – амплитуда сигнала, К – коэффициент крутизны изменения частоты,  – девиация частоты.

При  эффективная полоса частот сигнала  возможности ЛЧМ сигнала определяются его функцией неопределенности

:

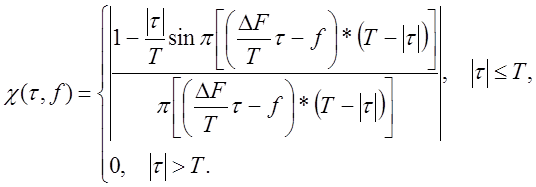            (16)

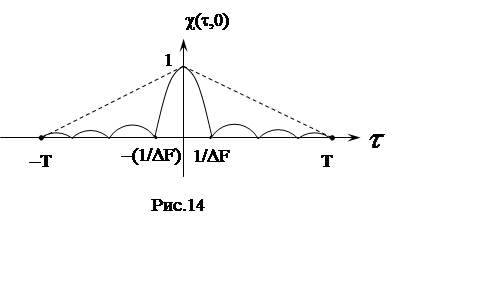
Функция  рис.14 является нормированной АКФ комплексной огибающей ЛЧМ сигнала.

 

функция 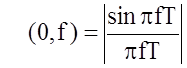 (рис. 15) представляет модуль спектральной функции прямоугольного видеоимпульса длительностью Т.

 

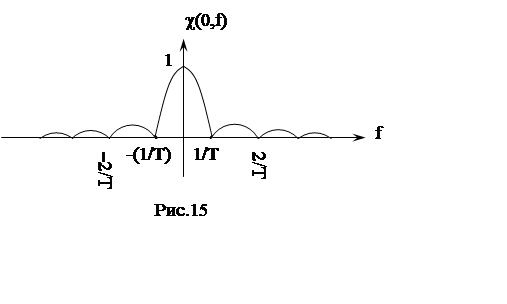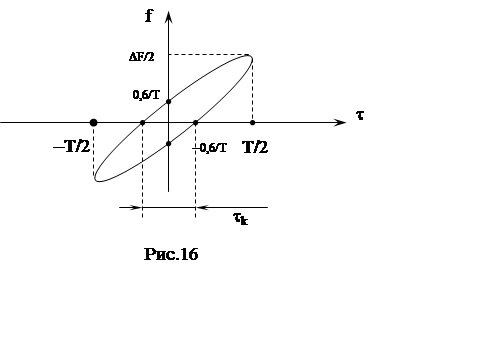
Диаграмма неопределенности ЛЧМ сигнала (рис. 16) – эллипс. Наклона которого относительно горизонтальной оси зависит от девиации частоты.

 

Из (16), рис. 14,15,16 следует:

время корреляции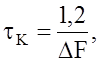

коэффициент сжатия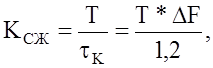

потенциальные точность и разрешающая способность по частоте определяются длительностью сигнала.

Широкое распространение получили псевдослучайные сигналы с дискретной фазовой модуляцией (ПС – сигналы). Аналитическое описание сигнала:

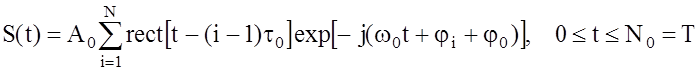  (17)

где  – длительность символа модулирующей функции,

N – количество символов в длительности Т сигнала,

 – дискретные значения фазы, привязанные к соответствующим значениям модулирующей функции.

Комплексная огибающая модулирующей функции:

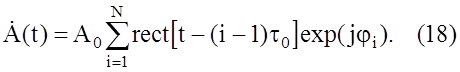
Действительная часть комплексной огибающей модулирующей функции:

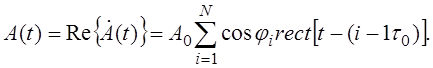                            (19)

Функцию  удобно выразить через символ  длительности  и модулирующая дискретная функция может быть представлена как ансамбль символов  Если последовательность символов носит псевдослучайный характер, то ее называют псевдослучайной последовательностью (ПСП), а сигнал имеющий такую модулирующую функцию – ПС – сигнал.

Если  принимает только два значения  радиан, то  и ПСП будет бинарной (двухуровневой). При  принимающей множество значений, ПСП будет многоуровневой (многофазной).

Спектрально – корреляционные свойства ПС сигнала с ДФМ полностью определяются модулирующей ПСП.

Ансамбли видеопоследовательностей можно отнести к классу ПСП, руководствуясь следующими свойствами:

Взвешенность. Характеризуется примерным равенством различных символов  на длительности Т.

АКФ последовательности близка к кнопочной функции, т.е. максимальный уровень бокового остатка существенно ниже уровня основного пика АКФ.

Спектральная плотность видеопоследовательность в пределах ее эффективной полосы должна быть по возможности равномерной.

Широкое применение в современных РТС с ПС – сигналами нашли бинарные ПСП. К ним относятся М-последовательности и четверично-кодированные последовательности (ЧКП).

Основные свойства М – последовательностей:

1. Это класс линейных рекуррентных последовательностей максимального периода, описываемые неприводимыми и примитивными полиномами n-й степени, вида

, где  – коэффициенты принимающие значения 0 или 1 , определяют количество символов n-значной комбинации, участвующих в формировании по рекуррентному правилу:

.                                                     (20)

Причём число членов  в (20) всегда чётное, а суммирование осуществляется по модулю два, если .

Сформированная по правилу (20) М-последовательность имеет значимость . Например, неприводимый и примитивный полином  описывает М-последовательность , а рекуррентное правило формирования символов имеет вид .

2. В одном периоде последовательности число символов разного значения (1 и 0) отличается на единицу.

3. В периоде последовательности содержатся все n-значные комбинации двоичного кода, кроме нулей.