Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений, страница 9

4. С помощью составленной программы найти приближенное решение ЗК

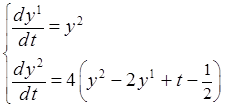, ,      , .                        (2)

с точностью  = 10^-4. Начальный шаг  = 0.1. Точки выдачи результатов tr(i) = 0.25i,   i = 1,…,10.

Найти точное решение ЗК (2) аналитически и сравнить его с приближенным в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 17

1. Привести расчетные формулы (безразностные) 4-шагового интерполяционного и 3-шагового экстраполяционного методов Адамса для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Изложить предиктор-корректор метод с двумя коррекциями (ПКМ2), основанный на паре указанных методов. Дать определение глобальной (методической) погрешности (ГП) ПКМ2. Привести асимптотическую формулу для ГП ПКМ2 и указать условия, при которых она верна. Сформулировать правило Рунге для практической (апостериорной) оценки ГП ПКМ2. При каких условиях оно применимо?

2. Описать алгоритм ПКМ2 с автоматическим выбором постоянного шага по заданной величине  ГП. Для вычисления приближенного решения в начальных узлах сетки использовать классический метод Рунге-Кутты 5) из [1, стр. 9]. ГП в текущем узле оценивать по правилу Рунге, решая ЗК (1) параллельно тем же ПКМ2 на сетке с половинным шагом. Если в некотором узле ГП оказывается , то нужно, не доводя интегрирование с принятым шагом до конца отрезка [, T], вернуться в начальную точку , уменьшить шаг вдвое и повторить расчет и т. д..

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – шаг начальной сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; hr – шаг, на котором получено решение с требуемой точностью .

4. С помощью составленной программы найти приближенное решение ЗК

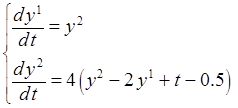,           ,      , .    (2)

с точностью  = 10^-5. Точки выдачи результатов tr(i) = 0.25i,   i = 1,…,10. Шаг начальной сетки  = 0.25.

Найти точное решение ЗК (2) аналитически и сравнить его с приближенным в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залёткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 18

1. Привести формулы явного трехэтапного метода типа Рунге-Кутты (МТРК) 3) [1, стр. 9] и трехшагового экстраполяционного метода Адамса (ЭМА) [1, стр. 12] для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) обоих методов; б) указать порядки их точности.

Сформулировать правило Рунге для практической (апостериорной) оценки ГП рассматриваемых методов. На чем основывается это правило и при каких условиях оно применимо?

2. Изложить алгоритм численного решения ЗК (1) с автоматическим выбором постоянного шага интегрирования по заданной величине  ГП, основанный на ЭМА. Для вычисления приближенного решения в начальных узлах сетки использовать МТРК. Глобальную погрешность оценивать по правилу Рунге, параллельно решая ЗК (1) с половинным шагом. Если в текущем узле ГП оказалась , нужно вернуться в начальный узел  и повторить процесс интегрирования, уменьшив шаг вдвое.

3. Составить программу, реализующую алгоритм из п. 2. В программе предусмотреть возможность решения ЗК (1) только по МТРК (но, как и в основном варианте, — с автоматическим выбором постоянного шага).