Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений, страница 10

Входные данные программы: , , , , , ;  – шаг начальной сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; hr – шаг, на котором получено решение с требуемой точностью .

Во входные данные, по-видимому, следует включить и признак (номер) метода, с помощью которого решается ЗК (1).

4. С помощью составленной программы двумя методами найти приближенное решение ЗК

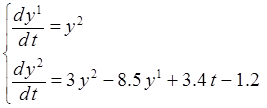,      ,         , .                   (2)

с точностью  = 10^-4. Начальный шаг  = 0.2. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10.

Решить ЗК (2) аналитически и сравнить точное решение с приближенными в точках выдачи.

Подсчитать число обращений к вычислению правой части системы (2) в обоих методах.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 19

1. Привести формулу явного двухэтапного метода типа Рунге-Кутты (МТРК) №1 из [1, стр. 8] и формулы двухшагового и трехшагового экстраполяционных методов Адамса (ЭМА) [1, стр. 12] для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) локальных погрешностей (ЛП) этих методов в узле ; б) указать порядки их точности (определив предварительно понятие порядка точности).

Сформулировать правило Рунге для апостериорной оценки ЛП используемого метода типа Рунге-Кутты и правило для апостериорной оценки локальной погрешности двухшагового метода Адамса с помощью трехшагового. На чем основаны эти правила и при каких условиях они применимы?

2. Изложить алгоритм численного решения ЗК (1), основанный на двухэтапном методе типа Рунге-Кутты и двухшаговом методе Адамса из п. 1. Шаг численного интегрирования переменный и выбирается из условия, что локальная погрешность в текущем узле должна быть меньше заданной величины . Решение в первых четырех узлах вычисляется по методу Рунге-Кутты с оценкой локальной погрешности по правилу Рунге. Если шаг интегрирования при этом оставался постоянным, то решение в следующих узлах строится по двухшаговому методу Адамса с контролем его локальной погрешности с помощью трехшагового метода Адамса. Интегрирование по методу Адамса происходит до тех пор, пока локальная погрешность не станет . При этом нужно вернуться на шаг назад и продолжать интегрирование по методу Рунге-Кутты до тех пор, пока не будут сделаны подряд 3 одинаковых шага с локальной погрешностью . Если это произошло, нужно перейти на метод Адамса и т. д.

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи приближенного решения; tr(1), tr(2), …, tr() – точки выдачи приближенного решения (они должны быть узлами сетки).

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; hk – последний шаг сетки.

4. С помощью составленной программы найти приближенное решение ЗК

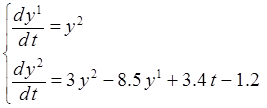,      ,         , .                   (2)

с локальной погрешностью, не превосходящей  = 10^-5. Начальный шаг  = 0.2. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10.

Решить ЗК (2)  аналитически и сравнить точное решение и приближенное в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 20

1. Привести расчетную формулу классического метода Рунге-Кутты [1, стр. 9, метод 5)] для нахождения приближенного решения ЗК