Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений, страница 3

Как связан порядок точности ЭМА с числом узлов (шагов) в его формуле? Изложить практический способ оценки ГП ЭМА с помощью метода более высокого порядка точности. На чем основан этот способ и при каких условиях он применим?

2. Конкретизировать параметры и вид 3- и 4-шагового ЭМА. Изложить алгоритм 3-шагового ЭМА с автоматическим выбором постоянного шага сетки по заданной величине  глобальной погрешности. Последнюю оценивать, решая ЗК (1) параллельно 4-шаговым ЭМА.

Для вычисления приближенного решения в начальных узлах использовать МТРК 5) из [1, стр. 9].

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – шаг начальной сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов (эти точки должны быть узлами сетки).

Выходные результаты: tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи, hr – шаг сетки, на которой получено решение с точностью .

4. С помощью составленной программы найти приближенное решение ЗК

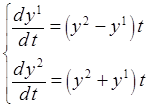,     ,         , .                                      (2)

с точностью  = 10^-4. Шаг  начальной сетки – 0.1. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10.

Добавление

Найти решение ЗК (2) аналитически и сравнить с приближенным в точках выдачи (т. е. привести таблицы обоих решений).

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залёткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 6

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК в узле .

Из каких соображений выбираются параметры общей формулы при получении конкретного МТРК? Что такое порядок точности МТРК?

Как оценить ГП МТРК с помощью МТРК более высокого порядка? На чем основывается такой способ оценки ГП МТРК и при каких условиях он применим? (См. [1, стр. 19-21].)

2. Изложить алгоритм решения ЗК (1) с помощью 2-х МТРК порядка точности q и q+1 с автоматическим выбором постоянного шага сетки по заданной величине  ГП [1, стр. 21]. ГП оценивать так, как указано в п. 1.

3. Составить программу, реализующую алгоритм из п. 2 для пары МТРК 4) и 6) из [1, стр. 9].

Входные данные программы: , , , , , ;  – начальный шаг интегрирования;  – минимальный допустимый шаг интегрирования;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; N – число узлов сетки, на которой достигнута требуемая точность  приближенного решения.

4. С помощью составленной программы найти приближенное решение ЗК

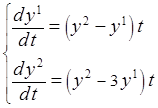,   ,         , .                                      (2)

с точностью  = 10^-4. Шаг начальной сетки  = 0.15,  = 10, tr(i) = 0.3i,   i = 1,…,10.

Найти точное решение ЗК (2) аналитически и вывести на печать таблицу его значений в точках tr(i),   i = 1,…,10.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 7

1. Привести формулу метода Мерсона (метод 8 в [1, стр. 9 и 23]) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) этого метода; б) локальной погрешности (ЛП) этого метода.