Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 1

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК в узле .

Из каких соображений выбираются параметры общей формулы для получения конкретного метода? Сформулировать правило Рунге для практической оценки ГП и ЛП МТРК. На чем основывается это правило и при каких условиях оно применимо?

2. Конкретизировать параметры общей формулы и ее вид для классического метода Рунге-Кутты, а также правило Рунге для оценки ГП и ЛП этого метода. Изложить алгоритм этого метода с автоматическим выбором переменного шага интегрирования по заданной величине  локальной погрешности.

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг интегрирования;  – минимальный допустимый шаг интегрирования;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; ge – максимальное значение глобальной погрешности метода; tge – точка в которой это значение достигается.

Локальную погрешность оценивать по правилу Рунге, глобальную по тому же правилу, интегрируя параллельно систему (1) с «половинным» шагом.

Приближенное значение решения в точке выдачи tr(i), расположенной между соседними узлами сетки , , вычислять с помощью интерполяционного полинома Эрмита (почему?), построенному по приближенным значениям , .

4. С помощью составленной программы найти приближенное решение ЗК

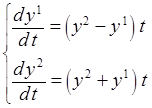,     ,         , .                          (2)

с ЛП  = 10^-5. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залёткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 2

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК в узле .

Из каких соображений выбираются параметры общей формулы для получения конкретного МТРК? Сформулировать правило Рунге для практической (апостериорной) оценки ГП и ЛП МТРК. Как оценивать эти погрешности с помощью метода более высокого порядка? На чем основываются все упомянутые оценки и при каких условиях они применимы?

2. Конкретизировать параметры и вид формул МТРК 4) и 6) из [1, стр. 9]. Изложить алгоритм численного решения ЗК (1) с автоматическим выбором постоянного шага интегрирования по заданной величине  ГП.

Метод 4) является основным в алгоритме, метод 6) используется для оценки ГП первого метода. Решать ЗК рекомендуется параллельно обоими методами, переходя сразу к половинному шагу (и возвращаясь в точку ), как только в текущем узле ГП превысит .

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг интегрирования;  – минимальный допустимый шаг интегрирования;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; ; hr – шаг, при котором получено решение с требуемой точностью.

4. С помощью составленной программы найти приближенное решение ЗК

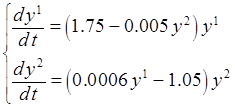,            ,         , .   (2)

с точностью  = 0.1. Начальный шаг  = 0.15. Точки выдачи результатов tr(i) = 0.3i,   i = 1,…,10.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 3

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК в узле .

Из каких соображений выбираются параметры общей формулы для получения конкретного метода? Что такое порядок точности МТРК?

Сформулировать правило Рунге для практической (апостериорной) оценки ГП и ЛП МТРК. На чем основывается это правило? Как оценивать локальную погрешность МТРК с помощью метода более высокого порядка точности? При каком условии данный метод называется вложенным по отношению к методу более высокого порядка?