Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений, страница 11

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной погрешности (ГП) этого метода; б) локальной погрешности (ЛП) этого метода;

в) его порядка точности.

Указать порядок точности метода, привести асимптотическую формулу для его глобальной погрешности. При каких условиях эта формула имеет место?

Сформулировать правило Рунге для практической оценки ГП метода. На чем основывается это правило и при каких условиях оно применимо?

2. Изложить алгоритм приближенного решения ЗК (1) классическим методом Рунге-Кутты с автоматическим выбором постоянного шага интегрирования по заданной величине  ГП. Последнюю оценивать по правилу Рунге только в заданных точках выдачи tr(1), tr(2), …, tr(), вычислив решение сначала на сетке с шагом , а затем – с шагом /2. (Точки выдачи должны быть узлами сетки.)

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – шаг начальной сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; hr – шаг сетки, обеспечивающий требуемую точность приближенного решения.

4. С помощью составленной программы найти приближенное решение ЗК

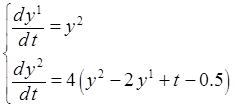,           ,      , .    (2)

с точностью  = 10^-5. Шаг начальной сетки  = 0.125. Точки выдачи результатов tr(i) = 0.125i,   i = 1,…,20.

Найти точное решение ЗК (2)  аналитически и сравнить его с приближенным в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 21

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК в узле .

Из каких соображений выбираются параметры общей формулы при получении конкретного МТРК? Что такое порядок точности МТРК?

Сформулировать правило Рунге для практической (апостериорной) оценки ГП и ЛП МТРК. На чем основывается это правило и при каких условиях оно применимо?

2. Выписать таблицу параметров МТРК 3) из [1, стр. 9] и оценку его ЛП по правилу Рунге. Изложить алгоритм решения ЗК (1) по этому методу с автоматическим выбором переменного шага интегрирования по заданной величине  локальной погрешности. Последнюю оценивать по правилу Рунге.

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг интегрирования;  – минимальный допустимый шаг интегрирования;  – число точек выдачи приближенного решения; tr(1), tr(2), …, tr() – точки выдачи приближенного решения.

Выходные результаты: tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; N – число узлов сетки.

Приближенное значение решения в точке выдачи tr(i), не совпадающей с узлами сетки и расположенной, например, между соседними узлами сетки , , вычислять с помощью интерполяционного полинома Эрмита (почему?), построенному по приближенным значениям , .

4. С помощью составленной программы найти приближенное решение ЗК

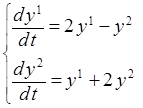,      ,         , .                                      (2)

Локальная погрешность не должна превосходить  = 10^-5. Начальный шаг  = 0.1,  = 10^-4. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10.

Решить ЗК (2)  аналитически и сравнить таблицы приближенного и точного решений.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залеткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.