Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений, страница 8

4. С помощью составленной программы найти приближенное решение ЗК

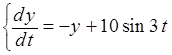,             ,         .                                          (2)

с  = 10^-5; Начальный шаг  = 0.2; Точки выдачи tr(i) = 0.2i,   i = 1,…,10.

Найти решение задачи (2) аналитически и сравнить точное и приближенное решение в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залёткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 15

1. Привести общий вид безразностных формул экстраполяционного метода Адамса (ЭМА) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) ЭМА; б) порядка точности ЭМА.

Как связан порядок точности ЭМА с числом узлов (шагов) в его формуле? Изложить практический способ оценки ГП ЭМА с помощью метода более высокого порядка точности. На чем основан это способ и при каких условиях применим?

2. Конкретизировать параметры и вид 4- и 5-шагового ЭМА. Изложить алгоритм 4-шагового ЭМА с автоматическим выбором постоянного шага сетки по заданной величине  глобальной погрешности. Последнюю оценивать, решая ЗК (1) параллельно 5-шаговым ЭМА. Для вычисления приближенного решения в начальных узлах использовать метод Рунге-Кутты 6) из [1, стр. 9].

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг интегрирования;  – минимальный допустимый шаг интегрирования;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов (эти точки должны быть узлами сетки).

Выходные результаты: tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; ; hr – шаг, на котором получено решение с точностью .

4. С помощью составленной программы найти приближенное решение ЗК

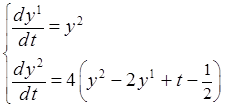,             ,         , .                   (2)

с точностью  = 10^-4. Точки выдачи результатов tr(i) = 0.2i,   i = 1,…,10. Шаг начальной сетки  = 0.1.

Замечание

Решение ЗК (2) можно найти аналитически и сравнить с приближенным в точках выдачи.

Литература

1. Методические указания по вычислительному практикуму. Ч.3., Л. 1984
2. Арушанян О.Б., Залёткин С.Ф. Численное решение ОДУ на Фортране., МГУ, 1990.

Тема 5. Численное решение задачи Коши (ЗК) для системы обыкновенных дифференциальных уравнений.

Задание 16

1. Привести общий вид формулы явного -этапного метода типа Рунге-Кутты (МТРК) для нахождения приближенного решения ЗК

,                      (1)

где  – искомая, а  – заданная вектор-функции, – заданный вектор.

Дать определения:

а) глобальной (методической) погрешности (ГП) МТРК; б) локальной погрешности (ЛП) МТРК.

Из каких соображений выбираются параметры общей формулы для получения конкретного МТРК? Сформулировать правило Рунге для практической (апостериорной) оценки ГП и ЛП МТРК. Как оценивать эти погрешности с помощью метода более высокого порядка? На чем основываются все упомянутые оценки и при каких условиях они применимы? (См. [1, стр. 19-21].)

2. Конкретизировать параметры и вид формул МТРК 2) и 3) из [1, стр. 8, 9]. Изложить алгоритм численного решения ЗК (1) с автоматическим выбором постоянного шага сетки по заданной величине  ГП. Метод 2) является основным в алгоритме; метод 3) используется для оценки ГП первого метода и применяется параллельно (одновременно) с первым. Как только в некотором узле ГП становится , интегрирование нужно начинать с , уменьшив вдвое шаг сетки.

3. Составить программу, реализующую алгоритм из п. 2.

Входные данные программы: , , , , , ;  – начальный шаг сетки;  – минимальный допустимый шаг сетки;  – число точек выдачи результатов; tr(1), tr(2), …, tr() – точки выдачи результатов.

Выходные результаты: ; tr(1), tr(2), …, tr(); yr(1), yr(2), …, yr() – приближенные значения искомого решения  в точках выдачи; hr – шаг, на котором получено решение с требуемой точностью .