Анализ и синтез механизма стана холодной калибровки труб, страница 8

Сила F_c действует при рабочем ходе ползуна.  Находим значение М_пс в расчётном положении механизма:

Значения М_пс в остальных положениях механизма приведены в таблице 3.1.

3.2. Определение приращения кинетической энергии механизма. Построив динамическую модель исследуемого механизма, приступим к ее анализу. Анализ динамической модели будем проводить с помощью графоаналитического метода Виттенбауэра. Для построения диаграммы необходимо знать законы изменения приведенного момента инерции I_п и приращения кинетической энергии Т. Найдем закон изменения приращения кинетической энергии.

Сначала, в соответствии с (3.5)  и таблицей 3.1 строим график функции М_пс = f(j₁). При построении графика М_пс = f(j₁) координатную систему располагаем в начале рабочего хода исследуемого механизма (Рис. 3.2). Затем находим работу А_с приведенного момента сил сопротивления М_пс. Работу А_с определяем численным интегрированием функции М_пс=f(j₁). Интегрирование проводим, используя метод трапеций, в соответствии с которым

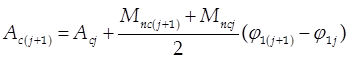         ,                          (3.6)

здесь j = 0,1,… - номер положения механизма, для которого вычисляется работа. В начальном положении А_с = 0.

Значения А_с, найденные по формуле (3.6), заносим в таблицу 3.1 и по ним строим график функции А_с = f(j₁) (Рис.3.2).

В установившемся режиме работа А_с приведенного момента сил сопротивления  за цикл равна работе приведенных движущих сил А_пд. Считая, что привод  развивает  постоянный по величине приведенный момент движущих сил М_пд, найдем его величину:

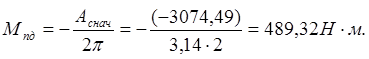
Знак минус указывает на то, что момент М_пд направлен на преодоление приведенного момента сил сопротивления М_пс. Строим график функции М_пд = f(j₁) (Рис. 3.2).

Работу А_д приведенного момента движущих сил М_пд вычисляем по формуле

                                                                     А_дi = М_пдj_1i,                                                      (3.7)  

где  i = 1, 2, … - номер положения механизма, для которого определяется работа А_д. В начальном (нулевом) положении А_д = 0.

Рассчитанные  по формуле (3.7) значения работы движущих сил А_д заносим в таблицу 3.1 и по ним строим график функции А_д = f(j₁) (Рис. 3.2).

Находим закон изменения приращения кинетической энергии Т, для чего алгебраически складываем работы А_д и А_с

,

где j = 0,1, 2… - номер положения механизма. Результаты вычислений заносим в таблицу 3.1 и по ним строим график зависимости Т = f(j₁) (Рис. 3.2).

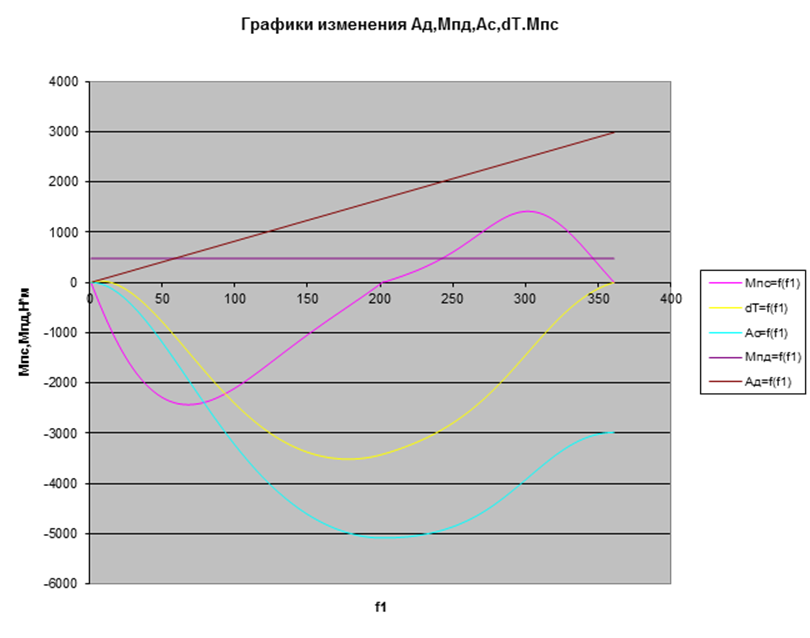
3.3. Определение момента инерции маховика. Подсчитываем величины с_jmax  и c_jmin соответственно:

 

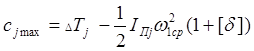                                                         ,                                       (3.8)

,

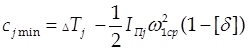где 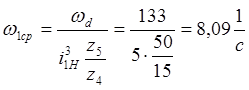  - средняя угловая скорость начального звена механизма.

Найденные значения с_jmax и c_jmin  заносим в таблицу 3.1. Из величин с_jmax выбираем наибольшую  величину  с_max = -777,43Дж,  а  из  c_jmin - наименьшую c_min = -4218,49Дж.

Момент инерции подсчитываем по формуле:

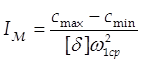                                                                                                              (3.9)

Подставляя исходные данные в формулу (3.9), получим:

.

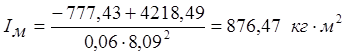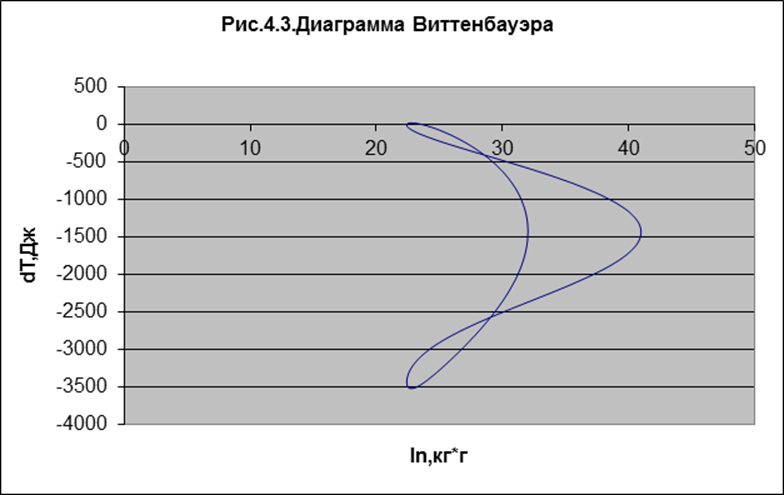
3.4. Определение закона движения начального звена и момента инерции маховика по диаграмме Виттенбауэра. Диаграмму Виттенбауэра строим в системе координат Т = f(I_п)  (Рис. 3.3), точки на диаграмме получаем, откладывая значения координат I_пj и Т_j, которые берем из таблицы 3.1 при одном и том же значении обобщенной координаты j₁. Построение диаграммы ведем, во,         ,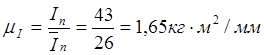

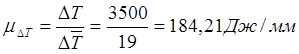где  - отрезки, изображающие на диаграмме истинные значения момента инерции и приращения кинетической энергии.

Вычисляем углы y_max  и y_min наклона касательных к диаграмме Виттенбауэра, при реализации которых в механизме будет обеспечена требуемая неравномерность движения:

,

.

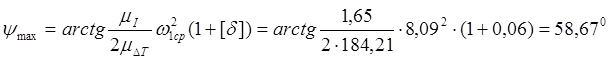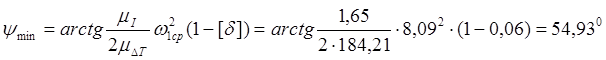Проводим под углами y_max  и y_min  к оси I_п касательные к диаграмме Виттенбауэра до пересечения с осью I_п в точках a и b.

Необходимый момент маховика подсчитываем по формуле

.

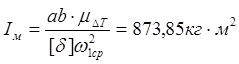3.5.  Определение угловой скорости и углового ускорения начального звена   механизма. Угловую скорость звена приведения механизма находим по следующей формуле:

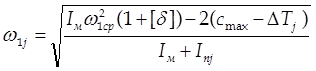.                               (3.10)

Для исследуемого механизма угловая скорость в расчетном положении определится:

.

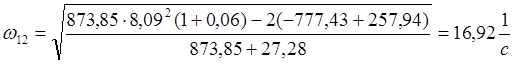Для определения углового ускорения e₁ запишем дифференциальное уравнение движения звена приведения:

.

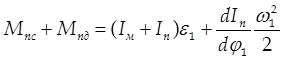Из последнего уравнения находим e₁

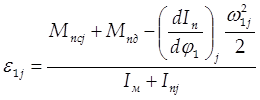                                                            .                                 (3.11)

Тогда угловое ускорение e₁ исследуемого механизма в расчётном положении определится:

.

 

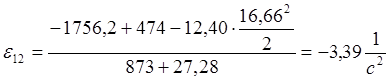Результаты  динамического анализа механизма