Анализ и синтез механизма стана холодной калибровки труб, страница 10

для звена 2:     F_И2x = - m₂ × а_S2x = -21 × 7,19 = -150.99 H,

                         F_И2y = - m₂ × а_S2y = - 21× (-40.65) = - 853.65 H,

                         М_И2 = - I_S2e₂ = - 0,15 × (-3.39) = 0.5085 H×м;

для звена 3:     F_И3x = - m₃ × а_S3x = - 120 ×(-4.79) = 574.8 H,

                         F_И3y = - m₃ × а_S3y = - 120 ×(-21,04) =2524 H,

                         М_И3 = - I_S3e₃ = - 0,38 ×(-3.39) =1.28 H×м;

для звена 5:     F_И5x =  - m₅ × а_S5y= - 1400 × (-5)= 7000 H,

                         F_И5y = 0

                         М_И5 = 0.

4.1.2. Силы, действующие на механизм. Для удобства дальнейшей работы в таблице 4.2 сведены все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.

 

Силы и моменты, действующие на механизм

Таблица 4.2

Силы веса, Н			Силы инерции, Н					Моменты сил инерции, Нм
F2y	F3y	F5y	FИ2x	FИ2y	FИ3x	FИ3y	FИ5x	МИ2	МИ3
-206,0	-1177,2	-13734	-150,99	853,65	574,8	2524	7000	0.5085	1.28

Так как направления сил и моментов учтены их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а  моменты – против часовой стрелки.

4.2. Определение уравновешивающего момента и реакций в кинематических  парах  аналитическим методом

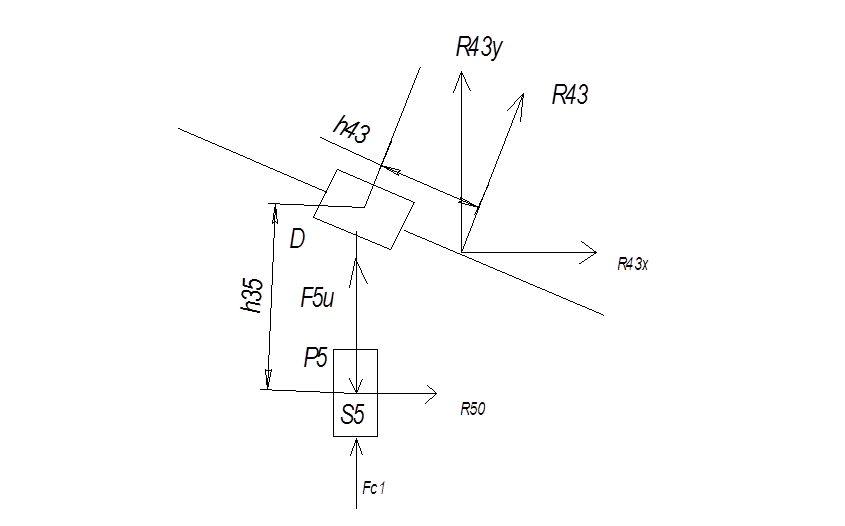
4.2.1. Силовой анализ структурной группы 4-5. Рисуем структурную группу 4-5 (Рис.4.1,а). Прикладываем к ней с целью упрощения вычислений в проекциях на оси действующие на нее силы.

1. Записываем в проекциях на оси координат условия равновесия всех сил:

  Fc1 - F_5y  + F_И5y +R_43y = 0,                                                                                      (4,2)

      R₅₀ + R_43X = 0.                                                                                                           

Из первого уравнения (4.1) находим R_43y:

R_43y= F_{5y -} F1 - F_И5y ) =13734-27000=-13266 Н,

  

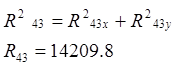Из второго уравнения (4.2) находим:

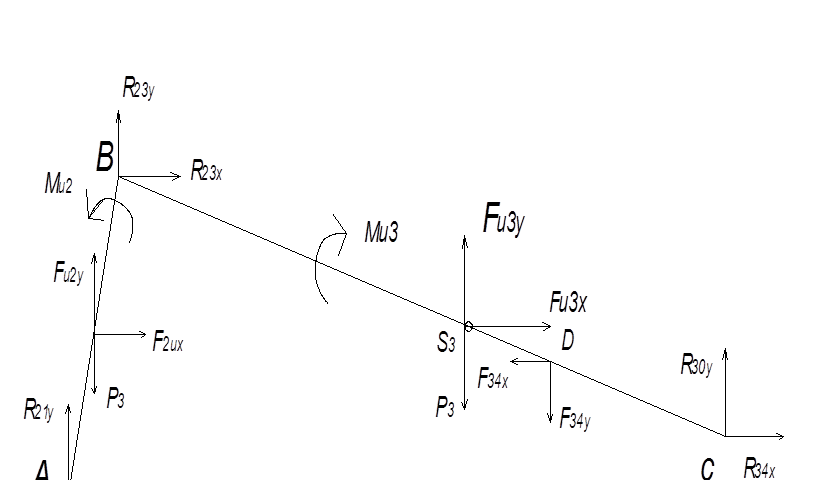
4.2.2. Силовой анализ структурной группы 2-3 (Рис. 4.1, б).Помимо заданных сил инерции, на группу действуют реакции R₂₁, R₃₀. Так же, чтобы не изображать отдельно звенья 2 и 3, в точке В прикладываем в проекциях на оси реакцию R_23. Силы представлены через их проекции на оси координат.

Для определения реакции в кинематических парах С и А записываем два уравнения проекций сил на координатные оси и два уравнения моментов  относительно точки В для звеньев 2 и 3:

 

(4.3)                                                                 

     

для звена 2: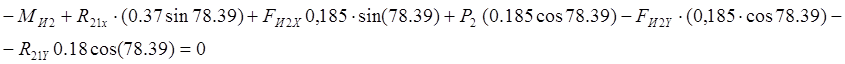

 для звена 3: 

 

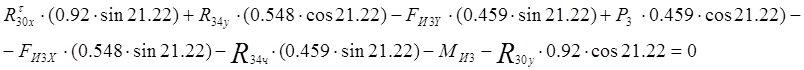
 В результате получим

;

;

;

Отсюда  выражаем:

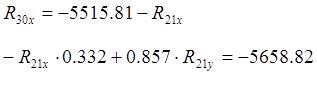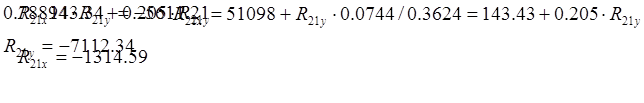Реакции R₂₁ и R₃₀ определятся соответственно:

  

 

 

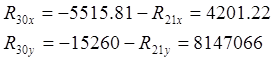                 (4,4)                                                                        

Реакцию R₂₃, действующую в кинематической паре В, находим из уравнения равновесия, например, звена 2:

   R_23x  + F_И2x + R_21x = 0,                                                                                      (4.5)                                                                      

    R_23y  + F_И2y -P₂ + R_21y = 0,

откуда 

R_23x  =- F_И2x - R_21x = 150.99+1314.59=1465.58 Н,

R_23y  =- F_И2y + P₂ - R_21y = 206.01+7112.34-853.65=6464.7 Н.

Полная реакция будет

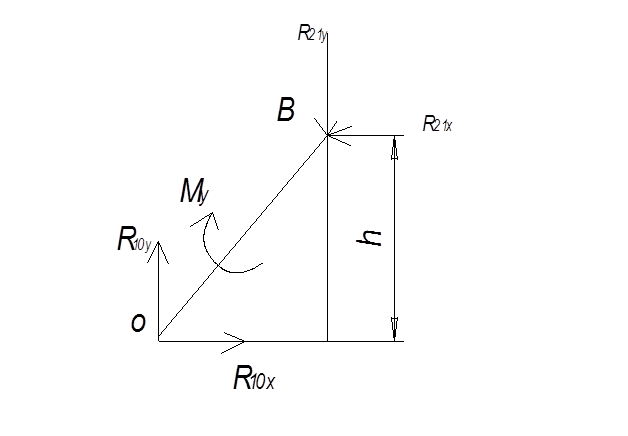
5.2.3. Определение уравновешивающего момента М_у и  реакции R₁₀  в кинематической паре О.

Для этого составляем уравнения равновесия начального звена механизма (Рис. 4.1, в). Эти уравнения имеют следующий вид:

                                                                                                       (4.6)

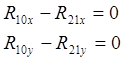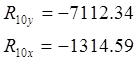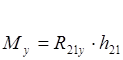 где h =cos33°×0.18=0.1492;

  М_у - уравновешивающий момент.

                                                 a)

 

                                                                  б)

в)

Рис.4.1. Силовой анализ механизма аналитическим методом

 

4.3. Определение уравновешивающего момента и реакций в кинематических парах графическим методом.

4.3.1. Силовой анализ структурной группы 4-5. Рисуем структурную группу 4-5 (Рис. 4.2, а) и прикладываем к ней все силы и моменты. Под действием приложенных сил и сил реакций структурная группа находится в равновесии. Подлежат определению реакции R₅₀  и R₄₃ во внешних кинематических парах, а также реакция R₄₅ во внутренней кинематической паре D.

Силовой анализ группы начинаем с определения касательной  составляющей реакции.

Определим реакции R₅₀  и R₄₃ из условия равновесия звеньев 4-5. Для этого запишем векторное уравнение сил, действующих на эту группу в целом.  Векторное уравнение записываем таким образом, чтобы неизвестные реакции находились по краям.

                                                         .                                  (4.7)                             

Уравнение (4.7) решаем графическим методом построения планов сил. Выбираем масштабный коэффициент сил m_F = 400 Н/мм. Находим для известных сил величины отрезков, которыми они изображаются на плане сил:

Истинные величины реакций находим следующим образом:

R₄₃ = cd×m_F = 35 ×400 = 14200 H;

R_50x = da×m_F = 12,5 × 400 = 5000 Н.

Данные, полученные в результате расчетов графическим и аналитическим методами, сводим в таблицу 4,3.

Результаты сго анализа структурной группы 4-5

Таблица 4.3

4.3.2. Силовой анализ структурной группы 2-3. Рисуем структурную группу 2-3 и прикладываем к ней все действующие силы и моменты (Рис.4.2, б). Реакции R₃₀ и R₂₁ изображаем разложенными на нормальные составляющие  и касательные  составляющие соответственно. Направление составляющих выбираем произвольно.

Силовой анализ группы начинаем с определения касательных  составляющих реакций. Для их определения составляем уравнение  моментов относительно точки С для звеньев 2 и 3 соответственно:

,

.

Выразив и подставив значения, получим:

=-9287,4Н

=153,815Н

Размеры длин звеньев берем из соответствующих планов положения механизмов.