Анализ и синтез механизма стана холодной калибровки труб, страница 3

1.18. Проводим классификацию структурных групп по И. И. Артоболевскому.

Элементарный механизм условно отнесен к механизму I класса.

Класс структурной группы определяется числом кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами.

Порядок группы определяется числом внешних кинематических пар.

Вид группы определяется в зависимости от места размещения на ней вращательных и поступательных кинематических пар.

Таблица 1.3.                       

№ п/п	Структурная схема	Номер звеньев, образующих группу	Класс	Порядок	Вид
1		0-1	I	-	-
2		2-3	II	2	1
3		4-5	II	2	5

1.19. Определяем класс сложного механизма стана. Механизм стана холодной калибровки труб относится ко II классу.

 

2. Кинематический анализ механизма стана холоной калибровки труб

Кинематический анализ любого механизма состоит в определении: крайних (мёртвых) положений стана; положений звеньев, включая и определение траекторий отдельных точек; скоростей и ускорений характерных точек звеньев по известному закону движения начального звена (обобщённой координаты). 

2.1. Определение крайних положений механизма аналитическим методом. Для исследуемого механизма крайними будут такие положения, когда кривошип и шатун то вытягиваются (ОАВ), то складываются (АОВ) в одну линию. 

2.1.1. Определим первое мёртвое положение (Рис.2.2.1(а)). Начало рабочего хода совпадает с крайним (мёртвым) положением (верхнее крайнее).

; 

Из DBCО найдём по теореме косинусов угол a:

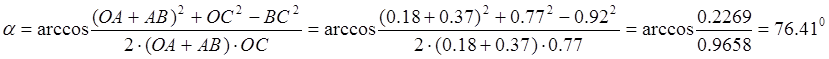
Определим угол b: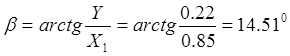       

Тогда

2.1.2. Определим второе мёртвое положение (крайнее нижнее) (Рис.2.2.1(б)), которое соответствует концу рабочего хода механизма.

; 

Из DОBC  найдём по теореме косинусов угол g:

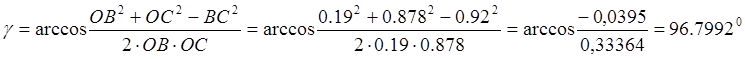
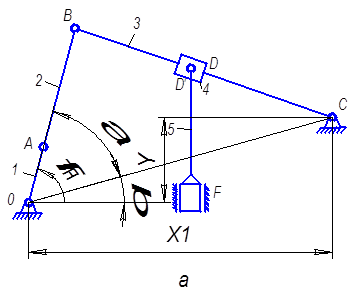
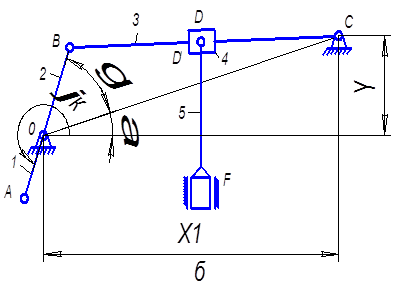
Рис. 2.1.Определение крайних положений механизма:

а – верхнее крайнее положение; б – нижнее крайнее положение

 

Определим угол a: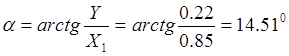        

Тогда

2.2. Для дальнейшего кинематического анализа, в частности, для определения положений звеньев и точек механизма, определения аналогов скоростей и ускорений графическим способом будем использовать промежуточный угол (j₁ = 90,92225°+30°=120,9225°). Аналитически будем проводить кинематический анализ для 12 положений механизма.

2.2.1. Кинематический анализ механизма в расчётном положении с помощью аналитического метода векторных замкнутых контуров.

Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещаем в точку О. Со звеньями механизма связываем векторы и получаем два замкнутых контура: ОАВСО и СEFDC. При образовании контуров следует учитывать, что в него должно входить не более двух неизвестных. Углы, определяющие положение звеньев (векторов), отсчитываем от положительного направления оси OX в направлении против хода часовой стрелки (Рис. 2.2).

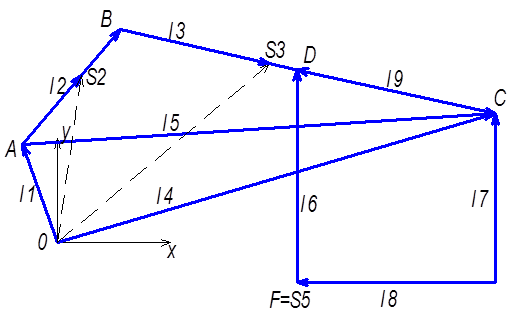
Рис. 2.2. Построение замкнутых векторных контуров

Записываем уравнение замкнутости первого контура:

l₁ + l₂ + l₃ - l₄ = 0                                                    (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

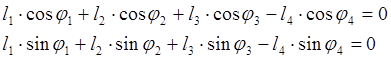                                                                      (2.2)

Среди величин, входящих в уравнения (2.2), переменными являются f₂, f₃, f_4. Угол f₁ является обобщённой координатой механизма  и поэтому он должен быть задан. Из уравнений (2.2) подлежат определению переменные параметры f₂, f₃ . Анализ системы уравнений (2.2) показывает, что система сложна для решения. Для упрощения нахождения углов f₂, f₃ вместо одного сложного контура ОАВСО рассмотрим два простых ОАСО и АВСА. Для этого введём в рассмотрение вспомогательный вектор l₅ , соединяющий точки А и С. При этом получим

l₁ + l₅ - l₄ = 0                                                           (2.3)

l₂ + l₃ - l₅ = 0                                                           (2.4)

Представим уравнение (2.3) в проекциях на оси координат:

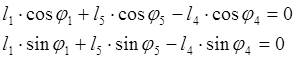                                                                                         (2.5)

 

Из уравнения (2.5) находим угол наклона вектора l₅, учитывая, что , м. для всех положений:

Так как вектор находится в первой четверти, то

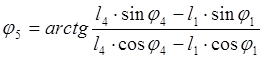
  ;                                                                                           (2.6)

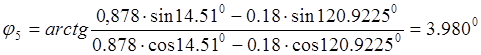
Найдём модуль вектора l₅:

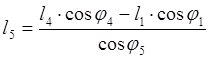;                                                                                                       (2.7)

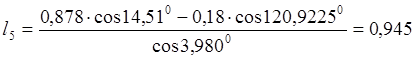м.

Углы f₂, f₃ находим из уравнения (2.4), записав его в проекциях на оси координат:

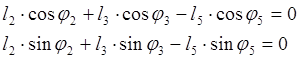      (2.8)                                                                                          

Слагаемые, содержащие угол f₃ , переносим в правую часть уравнений, возводим оба уравнения в квадрат и складываем. Получим           

                                                                      ,                                                        (2.9)

где 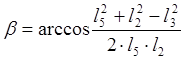   угол между векторами l₅   и  l₂ .

Для расчётного положения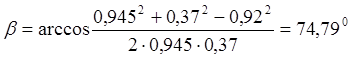

Для определения угла f₃ используем второе уравнение из системы (2.8):

Так как вектор находится в четвертой четверти, то

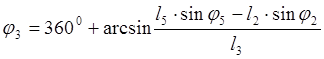,                                                                                (2.10)

.

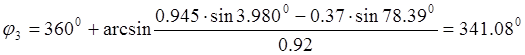Уравнение замкнутости второго контура:

                                                                                                         (2.11)

Представим уравнение (2.11) в проекциях на оси координат:

                                        

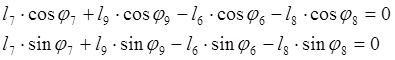                         (2.12)

      Среди величин, входящих в систему уравнений (2.12) переменными параметрами являются l₉ и l₇ . Из первого уравнения системы (2.12) найдём l₉, учитывая, что f₆ = f₇ =90⁰ ,     f₈ =180⁰ , f₉ =f₃ -180⁰ для всех положений:

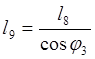                                                                                                                           (2.13)