Задачу решаем путем построения плана ускорений, считая w1 постоянной величиной:
1. Определяем ускорение точки А. Полное ускорение точки А равно
нормальной составляющей![]()
![]() ,
которая направлена по линии ОА к центру О.
,
которая направлена по линии ОА к центру О.
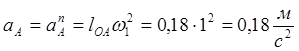 .
.
2. Из точки p - полюса плана ускорений - откладываем вектор, изображающий ускорение точки А, в виде отрезка pa = 50 мм (рис. 2.5).
3. Подсчитываем масштабный коэффициент ускорений:
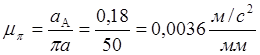 .
.
4. Для определения ускорения точки В записываем два векторных уравнения, рассматривая движение этой точки вначале со вторым звеном, а затем с третьим:
![]() ,
(2.37)
,
(2.37)
![]() .
.
Нормальные ускорения находим по формулам
![]()
![]()
Отрезки, изображающие векторы этих ускорений, равны:
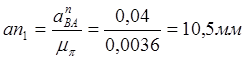 ,
,
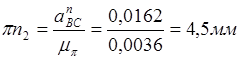 .
.
Через точки n1 и n2 плана ускорений проводим линии в направлении касательных ускорений, пересечение которых определяет точку b – конец вектора искомого ускорения точки В.
5. Для определения ускорения точки D1 используем теорему подобия:
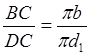 ;
; 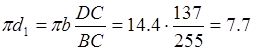
Ускорение точки D находится из уравнения:
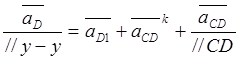 .
(2.38)
.
(2.38)
Кориолисово ускорение направлено перпендикулярно скорости VD1 :
![]() м.
м.
Уравнение решаем графически. Через точку d1 проводим линию, перпендикулярную CD, и откладываем на ней отрезок d1k, равный:
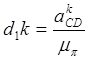 ;
; 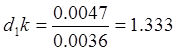 мм.
мм.
Через точку k проводим линию, параллельную CD, вдоль которой направлено относительное ускорение, а через ![]() - линию, параллельную y-y, вдоль которой направлено ускоре-
- линию, параллельную y-y, вдоль которой направлено ускоре-
ние точки D , точка пересечений этих линий есть d.
6. Из плана ускорений находим:
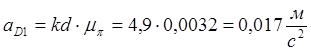
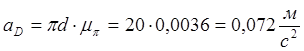 ,
,
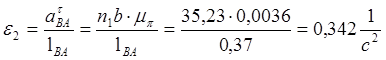 ,
,
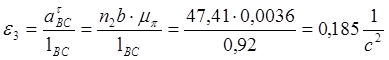 ,
,
.
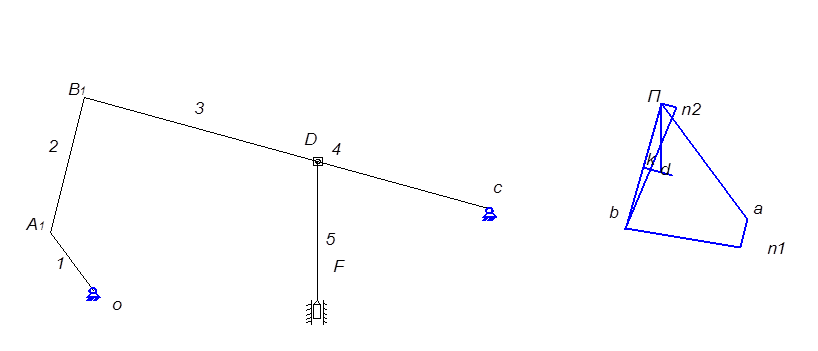 Рис 2.5. Планы ускорений
Рис 2.5. Планы ускорений
Так как при построении плана ускорений мы приняли w1 = сonst, то
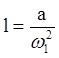 и
и 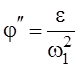 .
.
Учитывая, что
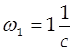 , находим
, находим
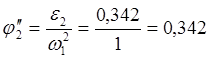
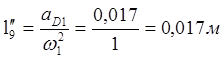
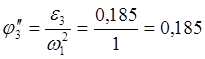 ,
,
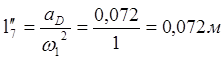 .
.
В таблице 2.7 приведены значения аналогов ускорений, полученные графическим и аналитическим методами.
Таблица 2.7
Результаты расчета аналогов ускорений
|
Величина |
j2'' |
j3'' |
l9'', м |
l7'', м |
|
Графически |
0.342 |
0,185 |
0,017 |
0,07 |
|
Аналитически |
0,344 |
0,18 |
0,016 |
0,069 |
|
Отклонение, % |
0.5 |
2.7 |
5,88 |
1.4 |
Аналогично проводим расчёт кинематических параметров в остальных положениях механизма.
3. РасчЁт маховика и динамическое
исследование машины
Динамический синтез механизма проводим с целью снижения колебаний величины угловой скорости начального звена, вследствие постоянного изменения нагрузок и неравномерности движения. Для снижения колебания угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу.
При определении момента инерции маховика Iм вместо реального механизма рассматривают его одномассовую динамическую модель. Динамическая модель механизма состоит из начального звена, к которому приложены движущие силы Мпд, а также приведены все силы (моменты) Мпс, действующие на звенья машины, и моменты инерции звеньев Iм. Начальное звено называется звеном приведения.
3.1. Определение параметров динамической модели. Для построения динамической модели механизма в качестве звена приведения выбираем начальное звено 1, к которому приводим все силы, действующие на механизм и моменты инерции подвижных звеньев. Исследуемая динамическая модель будет иметь вид:
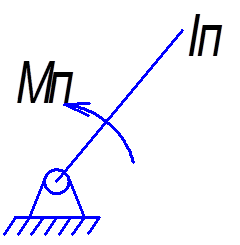
3.1.1. Находим приведенный момент инерции и его производную. Приведенный момент инерции определяется по формуле, которая имеет следующий вид:
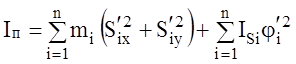 ,
(3.1)
,
(3.1)
где n – число подвижных звеньев, массы и моменты инерции которых заданы; mi – масса i-го звена; ISi – момент инерции i-того звена относительно оси, проходящей через центр масс; S¢ix, S¢iy – проекции на оси координат аналога скорости центра масс i-го звена; j¢i – аналог угловой скорости i-го звена.
Для рассматриваемого механизма стана холодной калибровки труб формула (3.1) принимает вид:
![]() , (3.2)
, (3.2)
где 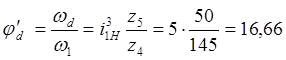 - аналог угловой скорости.
- аналог угловой скорости.
Дифференцируя по обобщенной координате j1 выражение (3.2), находим производную приведенного момента инерции
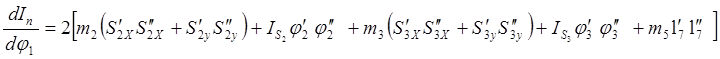
(3.3)
Подставив в (3.2) и (3.3) конкретные данные для механизма, находящегося во втором положении, найдем, что
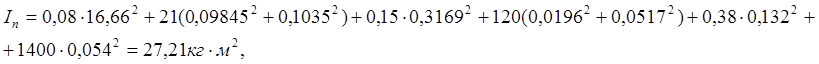
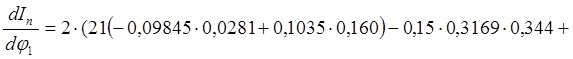
![]()
Считаем значения Iп и ![]() для остальных положений механизма.
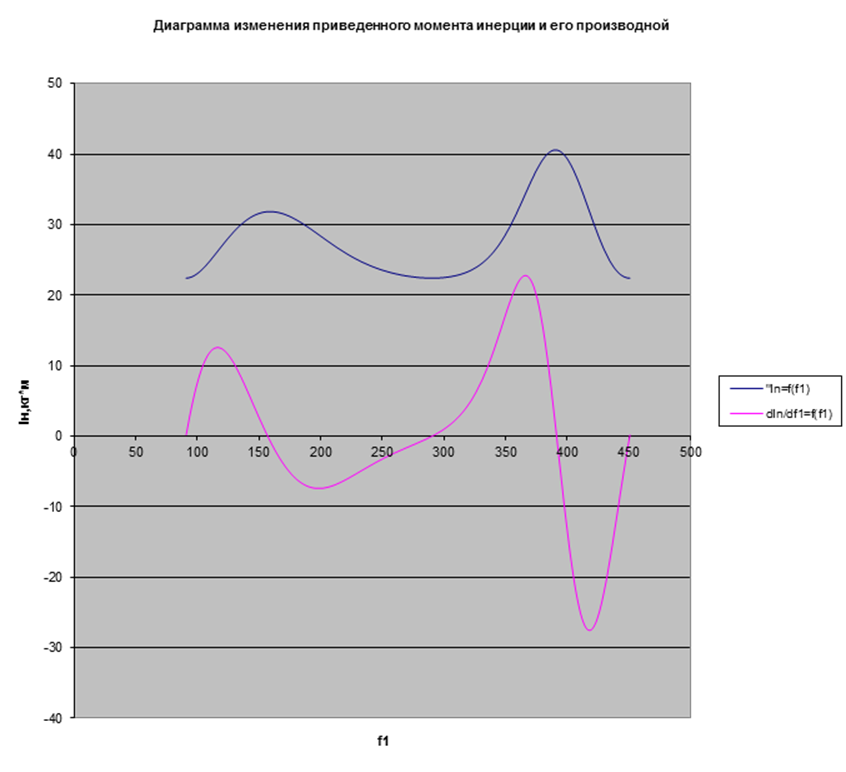
Полученные данные заносим в таблицу 3.1 и по ним строим графики функции Iп = f(j1) и
для остальных положений механизма.
Полученные данные заносим в таблицу 3.1 и по ним строим графики функции Iп = f(j1) и 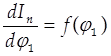 (Рис.
3.1). Начало координат графика размещаем в начале рабочего хода механизма.
(Рис.
3.1). Начало координат графика размещаем в начале рабочего хода механизма.
3.1.2. Находим приведенный момент сил сопротивления по формуле, которая имеет следующий вид:
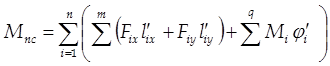 ,
(3.4)
,
(3.4)
где n – общее число подвижных звеньев; m – число сил F, действующих на i-е звено; Fix, Fiy – проекции силы на соответствующие оси координат; l¢ix, l¢iy – проекции на соответствующие оси координат аналога скорости точки приложения силы; q – число моментов М, действующих на
i-e звено.
Для исследуемого механизма формула (4.4) на рабочем и холостом ходе принимает вид соответственно:
Мпс = F2yS¢2y + F3yS¢3y + F5yl¢7 + Fc1l¢7 , (3.5)
Мпс = F2yS¢2y + F3yS¢3y + F5yl¢7 + Fc2l¢7
в этих формулах F2y, F3y – проекции на ось Y сил веса звеньев 2 и 3, которые соответственно равны:
F2y = - m2g = - 21×9,81 = - 206,01 H,
F3y = - m3g = - 120×9,81 = - 1177.2 H,
F5y = - m5g = - 1400×9,81 = -13734 H.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.