Анализ и синтез механизма стана холодной калибровки труб, страница 11

Нормальные составляющие будем находить графическим методом. Для этого составляем векторное уравнение сил, действующих на группу 2-3 в целом. Уравнение записываем таким образом, чтобы  неизвестные  величины находились на краях. При таких условиях векторное уравнение сил примет вид:

Выбираем масштабный коэффициент сил m_F = 25 Н/мм. Находим длины отрезков, изображающие на плане сил известные силы, входящие в уравнение:

;

;

;

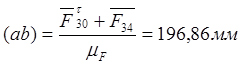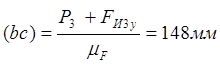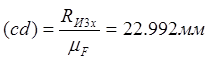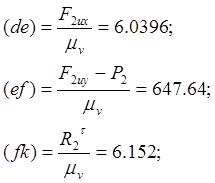Выбираем место на свободном поле чертежа и последовательно, начиная с отрезка ab (Рис.4.2, в), откладываем остальные отрезки в соответствии с векторным уравнением сил. Через точки a и k плана сил проводим линии действия нормальных составляющих  и . Точка l

пересечения этих линий определяет отрезки ea и de, изображающие реакции и . Истинное значение этих реакций определится:

= la × m_F = 89.96 × 25 = 2249.02H;

 = kl × m_F =285.47 × 25 = 7136.96 Н;

Суммируя графически и  находим полную реакцию R₃₀:

 =  7136.9 Н;

 = 9551.6 Н.

Аналогично .

Сравнительный анализ результатов графического и аналитического исследования структурной группы 2-3 приведен в таблице 4,4.

Сравнительный анализ графического и аналитического расчетов                        Таблица 4.4

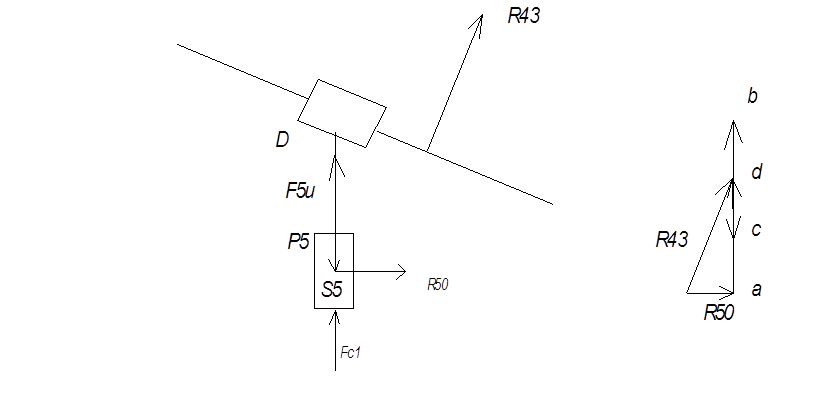
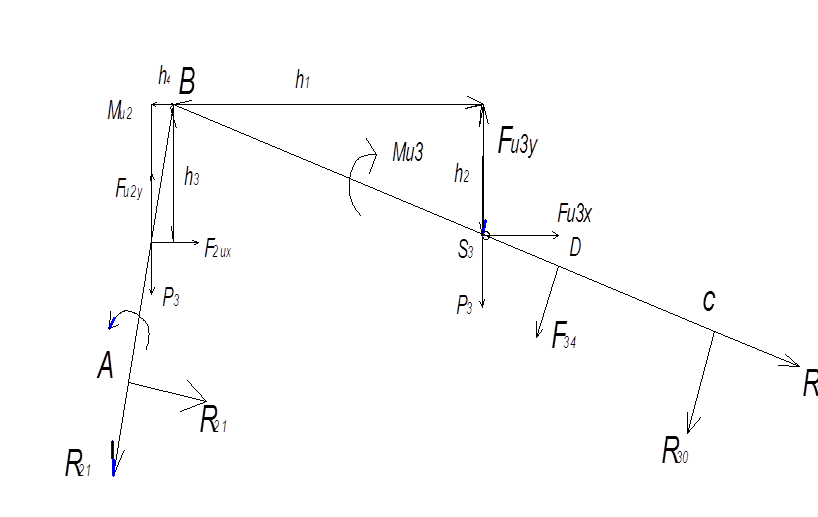
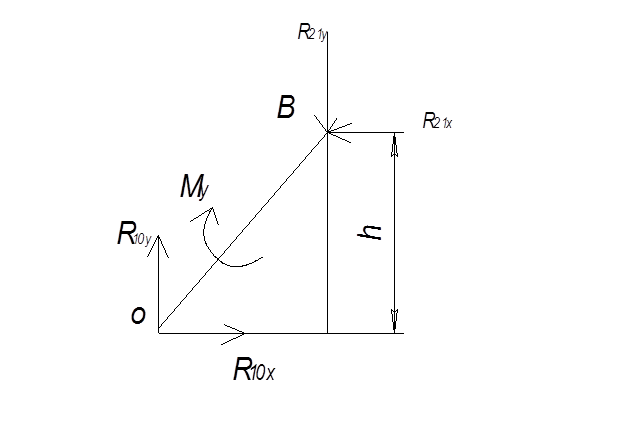
4.3.3. Силовой анализ начального звена. Рисуем начальное звено и прикладываем к нему все силы и моменты (Рис. 4.2, г). Здесь М_у – уравновешивающий момент.

Запишем уравнение суммы моментов относительно точки О:

М_у   -R₁₂h₁ = 0,

откуда

М_у =   R₁₂h₁ =7136.9×0.18 sin120.92° =1102.01 Н×м.

Для определения реакции R₁₀ в кинематической паре О запишем векторное уравнение сил, действующих на начальное звено:

R₁₂ + R₁₀ = 0

Строим план сил (Рис. 5.2, е) и находим истинное значение реакции R₁₀:

R₁₀ = -R₁₂= -7232 Н.

Находим погрешности определения реакции R₁₀   и  уравновешивающего  момента М_у соответственно:

,

.

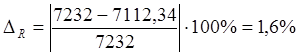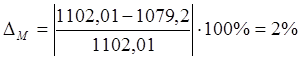Погрешности расчётов лежат в допускаемых пределах.

 

 

                                                  а)

                                                   б)

                                                  в)

     

                                                   г)

 Рис. 4.2. Силовой анализ механизма графическим методом

5. Определение уравновешивающего момента

методом рычага Жуковского

Теорема Жуковского гласит: «Если силу, приложенную к какой-либо точке звена механизма, перенести параллельно самой себе в одноименную точку повернутого плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности», то есть

М_р(F_i) = P_i,

где  М_р. – момент силы F_i относительно полюса плана скоростей, Р_i – мощность силы F_i.

Из законов динамики следует, что сумма мощностей всех внешних сил и сил инерции, приложенных к механизму, равна нулю, или

.

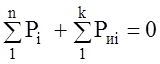В соответствии с теоремой Жуковского последнее уравнение равносильно уравнению относительно полюса повернутого плана скоростей, то есть

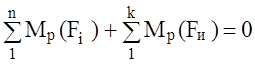                                                            .              (5.1)                              

Из уравнения (5.1) находится уравновешивающий момент.

Составим и решим  (5.1) для исследуемого механизма. Строим повернутый на 90° план скоростей механизма, к которому в соответствующих точках прикладываем заданные силы и силы инерции, сохраняя их истинные направления (Рис.5.1).

Моменты инерции  М_и1, М_и2 и М_и3 заменяем парами сил F_и1F¢_и1,  F_и2F¢_и2 и F_и3F¢_и3  соответственно, которые прикладываем перпендикулярно отрезкам ОА, АВ и ВС (Рис. 6.3, б) в кинематических парах О, А, В и С. Модули этих сил определятся:

;

;

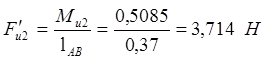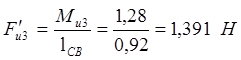Все силы переносим в одноименную точку плана скоростей без изменения ее направления. В точке а плана скоростей прикладываем неизвестную уравновешивающую силу F_y.

Записываем уравнение (6.1) моментов сил относительно полюса плана скоростей:

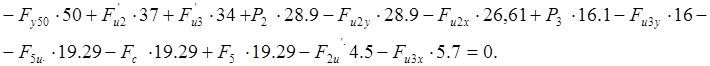      (5.2)           

Так как на рычаге Жуковского силы показаны в истинном направлении, при составлении уравнения их значения подставляем без учета знака.

Решив,  найдем F_у:

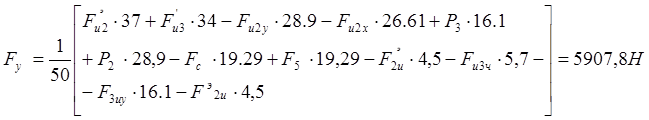
Зная величину F_y, найдем уравновешивающий момент М¢_y

М¢_y = F_y × l_OA = 5907,8 × 0,18 =1063,4  H×м.

Отклонение найденного с помощью рычага Жуковского значения момента М¢_y от определенного выше аналитическим методом определится:

,

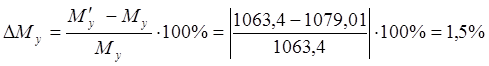что допустимо для инженерных расчетов .

 

 

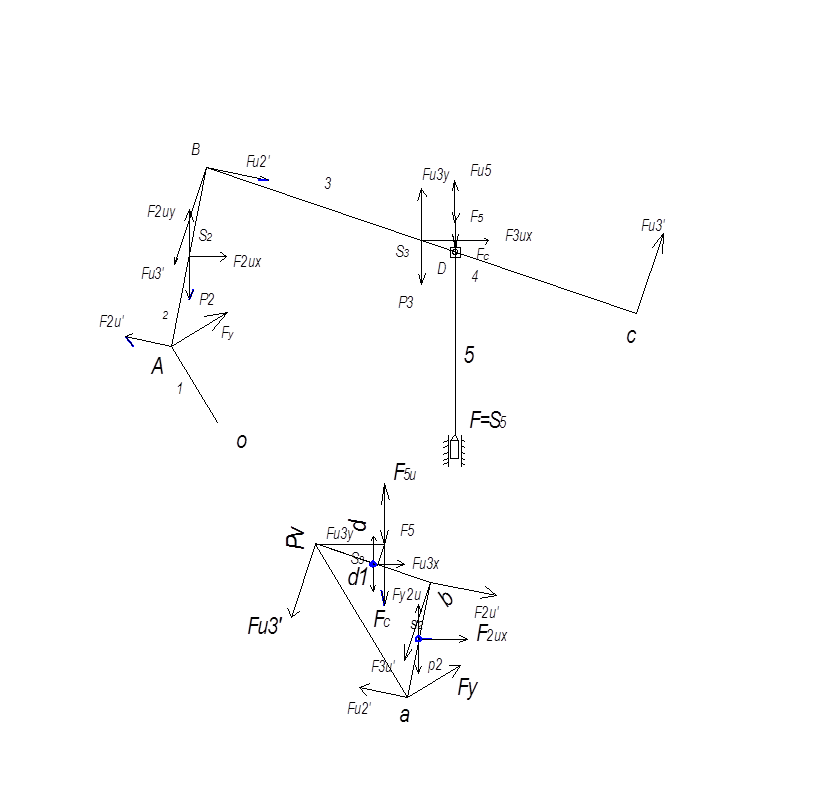Рис. 5.1. Рычаг Н.Е.Жуковского.

6. Синтез кулачковых механизмов

Синтез кулачковых механизмов заключается в определении основных размеров и профиля кулачка по заданному движению выходного звена.

Задача синтеза механизма решается в следующем порядке.

1.Зависимости аналога скорости и перемещения в функции угла поворота кулачка находятся интегрированием выражения аналога ускорения выходного звена.

2.Из условия ограничения угла давления или обеспечения выпуклости профиля кулачка определюется основные размеры кулачкового механизма.

3.Рассчитываются полярные координаты центрового профиля(Ro,ao)и рабочего профиля кулачка (Ri,ai).

Smax, мм	е, мм	jn°	jвв°	j­о°	Vd°
70	0	75	15	150	27

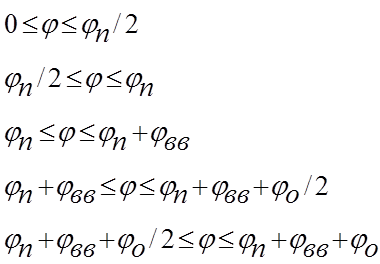
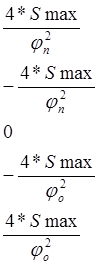
S``=                           

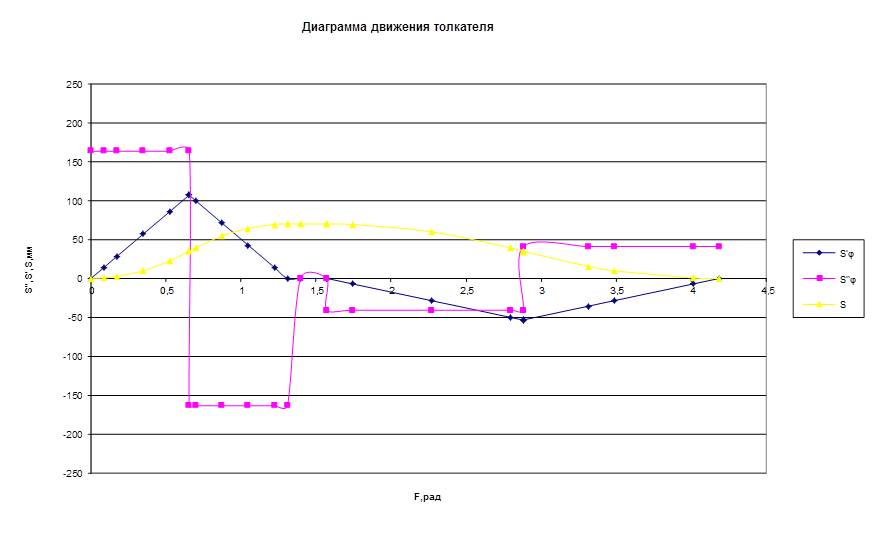
Проинтегрировав эти уравнения, получим выражение для определения аналога  скорости и перемещения толкателя.

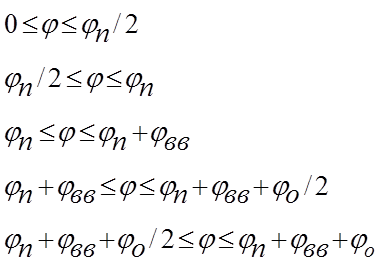
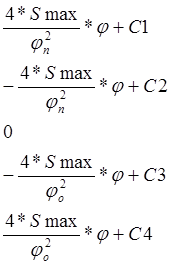
S`=

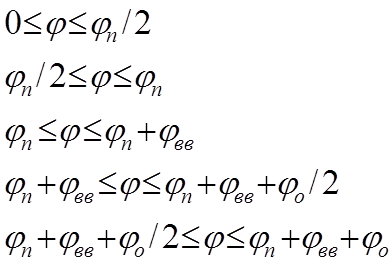
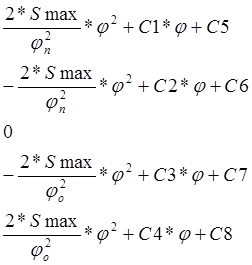
S=

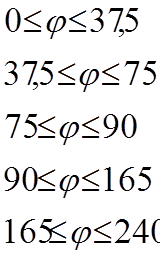После нахождения постоянных:

               163.57j

                  -163.57j+214

S`=              0.004083

               -40.89j+64.2

                40.89j-171.19

-

 

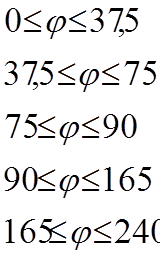
                        163.57j/2

                       -163.57j/2+214j-70

   S=                0.004083j+69.9

                     -40.89j/2+64.2j+19.5

                       40.89j/2-171.19j+358.26