Анализ и синтез механизма стана холодной калибровки труб, страница 5

3. Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

2.3.1. Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.12). После дифференцирования уравнений (2.2) получим                             

                                         -l₁j¢₁sinj₁ - l₂j¢₂sinj₂ - l₃j¢₃sinj₃ = 0,                            (2.19)

                                           l₁j¢₁cosj₁+ l₂j¢₂cosj₂ + l₃j¢₃cosj₃ = 0,

где j₁¢ - аналог угловой скорости звена 1. Принимаем j₁¢ = 1, так как угловая скорость звена 1 направлена против хода часовой стрелки; j₂¢ и j₃¢- аналоги угловых скоростей звеньев 2 и 3.

При дифференцировании уравнений (2.12) учитываем, что j₈ =const, j₉ =j₃ -180, а векторы`l₆ и l₈ не зависят от обобщенной координаты, в итоге получаем

                                         l¢₉cosj₉ – l₉j¢₉sinj₉ = 0,                                                             (2.20)

                                         l¢₇sinj₇ + l¢₉sinj₉ + l₉j¢₉cosj₉ = 0,

где l₇ – аналог абсолютной скорости точки F=S5.

Решаем систему уравнений (2.19) и находим  j₂^¢ и j₃^¢ :

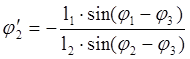,                                                                                                (2.21)

,

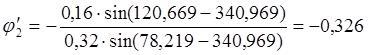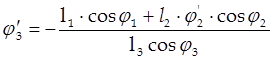,                                                                              (2.22)

.

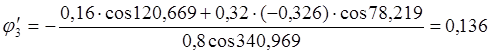Из системы уравнений (2.20) находим l₉^¢ и l₅^¢ :

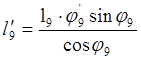,                                                                                                          (2.23)

,

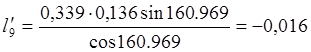l¢₇₌- l¢₉sinj₉ - l₉j¢₉cosj₉,                                                                                                    (2.24)

.

Аналоги скоростей центров масс звеньев 2 и 3 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения  (2.17) и (2.18):

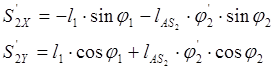                                           (2.25)

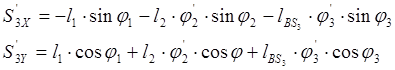                   (2.26)

Для расчётного положения:

                                                       

 

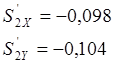
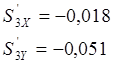
Аналоги скоростей для двенадцати положений механизма  представлены в таблице 2.4.

                                                                    Таблица 2.4.

            Аналоги скоростей для двенадцати положений механизма

Номер положения	j2',град	j3', град	l9', м	l7', м	S2x ', м	S2y ', м	S3y ', м	S3x ', м
Рас.	-0,31697	0,132404	-0,017682	0,054778	-0,09733	-0,1038	-0,05762	-0,01961
2	-0,12849	0,192454	-0,018019	0,075535	-0,06504	-0,16457	0,085915	-0,02112
3	0,076611	0,187547	-0,009824	0,070756	-0,01043	-0,17546	-0,08544	-0,011976
4	0,275768	0,142366	-0,00273	0,052867	0,043235	-0,1427	-0,06546	-0,003383
5	0,423255	0,087031	0,000354	0,032205	0,079687	-0,0838	-0,04015	0,00044
6	0,478225	0,052171	0,00079	0,019333	0,09048	-0,03811	0,023922	0,000942
Кон.	0,485287	-0,001537	-3,41E-05	-0,000572	0,084083	0,034554	0,000655	-4,232E-05
7	-0,46288	-0,277232	0,020673	-0,106589	-0,02204	0,201953	0,125149	0,0247424
8	-0,5892	-0,17477	0,022697	-0,071815	-0,05407	0,119779	0,076291	0,025373
9	-0,48647	1,41E-05	-2,151E-06	6,00E-06	-0,09067	-0,00146	-6,0E-06	-2,119E-06
10	-0,5535	-0,086825	0,012761	-0,03651	-0,07415	0,059236	0,03919	0,01371
11	-0,52034	-0,039198	0,005986	-0,016757	-0,08374	0,026465	0,01656	0,006480
12	-0,50628	-0,03958	0,005706	-0,016757	-0,08374	0,026465	0,01696	0,0064

   2.3.2. Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений  (2.19) и (2.20):

               - l₁cosj₁ - l₂j₂²sinj₂ - l₂(j₂^¢ )²cosj₂ –  l₃j₃²sinj₃ - l₃ (j₃^¢ ) ²cosj₃ = 0;               (2.27)

                  - l₁sinj₁ + l₂j₂²cosj₂ - l₂(j₂^¢ )²sinj₂ +  l₃j₃²cosj₃ - l₃ (j₃^¢ ) ²sinj₃ = 0,

  

                l²₉cosj₉ - l¢₉j¢₉sinj₉ – l¢₉j¢₉sinj₉- l₉j²₉sinj₉ - l₉(j¢₉) ²cosj₉  = 0;                    (2.28)

               l²₇sinj₇ + l¢₇j¢₇cosj₇ + l²₉sinj₉ +2 l¢₉j¢₉cosj₉+ l₉j²₉cosj₉ - l¢ ₉(j¢₉)²sinj₉= 0,

где j₂² и j₃²  - аналоги угловых ускорений звеньев 2 и 3,  l²₉ - аналог относительного ускорения точки D и l²₇ – аналог абсолютного ускорения точки F=S5.

Для определения j₂² и j₃²  решаем систему уравнений (2.27), отнимая в первом уравнении из аргументов всех тригонометрических функций угол j₃.

j²₂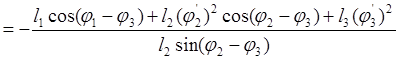,                                             (2.29)

j²₂,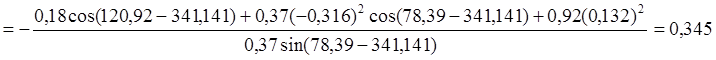                                               

j²₃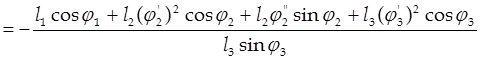,                             (2.30)

j²₃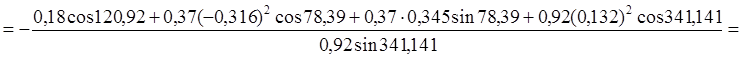

 

      Из системы уравнений (2.28) находим l₉²  и l₇² :

l₉²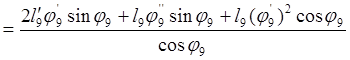                                                          (2.31)

l₉²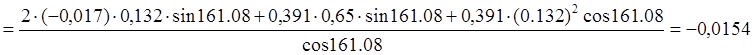

l₇^²=- l²₉sinj₉ -2 l¢₉j₉¢cosj₉- l₉j²₉cosj₉+ l¢₉(j₉¢)²sinj₉                                              (2.32)

l₇^²=

=0.069м.