Строительство и архитектура \ Конструкции из дерева и пластмасс

Проектирования деревянных элементов крыш с учетом традиционных и современных конструктивных индустриальных решений, страница 27

s^’=M_x/W_x=102:104=0,98 кН/см²=9,8 МПа <=

Расчёт на 2-е загружение от действия монтажной нагрузки Р=1,2 кН, которая вследствие подшитых снизу диагональных планок считается распределённой на ширину 0,5 м настила, или расчётную полосу настила в 1 м, ведём на 2Р. Изгибающий момент при изготовлении кровли

_xl²/8+0,21×2Plcos a =0,2×1,5²:14+0,21×2×1,2×0,995×1,5=0,78 кН×м, где =0,04+0,138+0,024=0,2 кН/м.

Напряжения изгиба в монтажной стадии

=M/W_x=78:104=0,75 кН/см²=7,5 МПа <=

Относительный прогиб от нормальной составляющей нагрузки

×10⁷×130,2×10^-8)= =1/254<=1/150.

Прочность и жёсткость настила обеспечены. Поперечные и диагональные планки прикрепляем к каждой доске настила двумя гвоздями 2´50 мм.

8 ОПТИМИЗАЦИЯ ПАРАМЕТРОВ КРОВЕЛЬНЫХ НАСТИЛОВ ПОСТРОЕЧНОГО ИЗГОТОВЛЕНИЯ

8.1 Одинарные сплошные настилы (рис. 8.1)

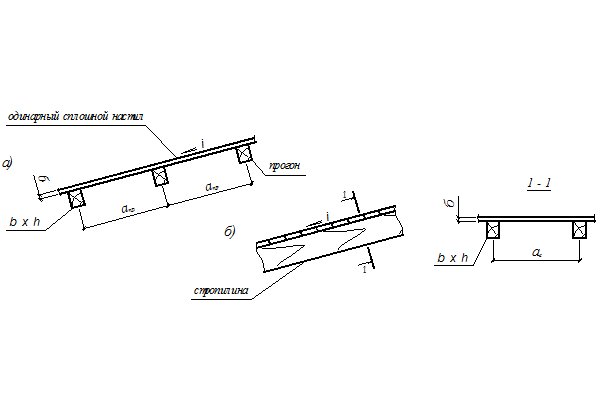
Рис. 8.1. Схема одинарного сплошного настила по прогонам или наслонным малоуклонным стропилам.

Рассмотрим сплошной одинарный настил, опертый на разрезные прогоны или малоуклонные стропила пролетом l. Выразим требуемый момент сопротивления одинарного прямого настила (l = a) для полосы шириной 1 м из условия прочности на 1-е загружение при

, откуда .

Для прогона при , откуда ; .

В качестве функции цели рассмотрим приведенный расход древесины на кровельный настил в м³/м², который вычисляется по формуле

, (8.1)

где (8.2)

. (8.3)

Условие минимума этой функции цели имеет вид

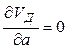; , откуда .

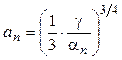После подстановки в эту формулу значений a_п и g и упрощений получаем формулу оптимального шага прогонов из условия прочности прямого настила на 1-е загружение

. (8.4)

Для косого сплошного настила = 1,414×а, и тогда

, откуда .

Функция цели в этом случае приобретает тот же вид , где . (8.5)

Условие оптимума в этом случае дает решение в виде формулы

. (8.6)

Во втором загружении изгибающий момент будем определять без учета постоянной нагрузки: при совместной работе всех досок при подшитом снизу бруске посередине пролета , и требуемый момент сопротивления в этом случае

, откуда

, при клавишной работе досок при b = 15 см

= 0,126 а и требуемый момент сопротивления отдельной доски

, откуда .

Приведенный расход древесины для 2-го загружения имеет вид

+=, где .

Взяв частную производную и приравняв ее к нулю, получаем уравнение , откуда .

После подстановки g и b и упрощений получаем формулу оптимального шага прогонов из условия прочности прямого настила при совместной работе на 2-е загружение

. (8.9)