|
Величина, единицы измерения |
Обрешетка из |
|
|
Бруска 50×100(h) |
Досок 175×40(h) |
|
|
Моменты сопротивления:
Моменты инерции:
Изгибающие моменты:
Напряжения при косом изгибе
То же, в МПа Расчетное сопротивление древесины
Условие прочности обрешетки выполняется ? Составляющие прогиба:
Полный прогиб в вертикальной плоскости
Относительный прогиб
Предельный относительный прогиб
Выполняется ли условие жесткости ? Приведенный расход древесины на обрешетку
Экономия древесины, % Технологичность варианта |
(5×102)/6=83,3 (10×52)/6=41,6 (5×103)/12=416,6 (10×53)/12=104,1 (0,771×2,12)/8=0,425 (0,257×2,12)/8=0,141 42,5/83,3+14,1/41,6= =0,51+0,34=0,85 8,5 13×0,95=12,35 Да (2,13×0,495×2,14)/ (384×107×104,1×10-8)= =0,0013 (2,13×0,165×2,14)/ (384×107×104,1×10-8)= =0,0017 0,132+0,172=0,22 0,22/210=1/954 1/150 Да (0,05×0,1)/0,25=0,02 ((0,028-0,02)/0,02)×100 =40 Ниже |
(17,5×42)/6=46,6 (4×17,22)/6=204,1 (17,5×43)/12=93,3 (4×17,53)/12=1786,4 (0,771×2,12)/8=0,425 (0,257×2,12)/8=0,141 42,5/46,6+14,1/204,1=0,91+0,07=0,98 9,8 13×0,95=12,35 Да |
|
(2,13×0,495×2,14)/ (384×107×93,3×10-8)= =0,0057 (2,13×0,165×2,14)/ (384×107×1786×10-8)= =0,0001 0,572+0,012=0,57 0,57/210=1/368 1/150 Да (0,175×0,04)/0,25= =0,028 Выше |
||
7.4 Расчет обрешетки род холодную ´´шиферную´´ кровлю
неотапливаемого склада
Исходные данные. Уклон кровли – 1:1, α=45º, àсбоцементные листы
54/200, шаг стропил – 1,2 м, г. Луцк, район по снегу 1 (s0=0.5 кПа), по ветру – III (W0=0,38 кПа).
Эскизный расчет обрешетки
Согласно изменениям к СНиП 2.01.07-85 снеговая нагрузка на кровле определяется по формуле sн=s0μ, где μ=cos1,8α , α=arctg i . В нашем случае α=45º , поэтому находим значение коэффициента μ по формуле:
μ=cos(1,8α)=cos(1,8·45º)=cos 81º = 0,1564. По старым нормам СНиП 2.01.07-85 μ = 1 при α = 25˚ и μ = 0 при α ≥ 60˚ . По интерполяции μ равен
![]() .
.
Таким образом, нормативная снеговая нагрузка на кровле
![]() кПа , расчетная снеговая нагрузка
кПа , расчетная снеговая нагрузка
![]() кПа .
кПа .
Эта нагрузка действует как распределенная по горизонтальной проекции кровли.
Ветровая нагрузка направлена нормально к поверхности кровли с аэродинамическим коэффициентом Сеl= +0,5 (см. прилож. 4 СНиП 2.01.07-85) .
Расчетная ветровая нагрузка на кровлю
![]() кПа .
кПа .
Собственная масса асбоцементных листов 54/200 толщиной 6 мм при массе листа 26 кг с учетом нахлестки (см. прилож. 3)
![]() кг/м2 .
кг/м2 .
Нагрузка от собственного веса
шифера составит ![]() 16∙9,8≈160 Н/м2= 0,16
кПа .
16∙9,8≈160 Н/м2= 0,16
кПа .
Расчетные нагрузки на обрешетку с максимальным шагом 1,5 м составляет:
нормальная составляющая –
![]() [0,16·1,2·0,707+
[0,16·1,2·0,707+
+0,9(0,34·0,7072+0,27)]1,5=0,771 кН/м ;
скатная составляющая –
![]() =[0,16·1,2·0,707+
=[0,16·1,2·0,707+
+0,9·0,34·0,707·0,707]1,5=0,407 кН/м ;
вертикальная составляющая –
![]() [0,16·1,2+0,9(0,34+0,27·0,707)]1,5=0,95
кН/м .
[0,16·1,2+0,9(0,34+0,27·0,707)]1,5=0,95
кН/м .
Здесь ψ=0,9 – коэффициент сочетаний для учета двух временных нагрузок от снега и ветра.
Изгибающий момент в вертикальной плоскости при 1-м загружении с учетом снега и ветра
![]() кН·м = 17,1 кНּсм, при 2-ом загружении с учетом
только временной монтажной нагрузки
кН·м = 17,1 кНּсм, при 2-ом загружении с учетом
только временной монтажной нагрузки
![]() = 0,332 кН·м = 33,2 кНּсм.
= 0,332 кН·м = 33,2 кНּсм.
Требуемые моменты сопротивления обрешетки при
![]() , так как i=1:1,
α=45º, ctg α=1,
cos α=sin α=0.0707
,
, так как i=1:1,
α=45º, ctg α=1,
cos α=sin α=0.0707
,
![]() 17,1(,0707+1·0,707)/(1,3·0,95)=18,55
см3 ;
17,1(,0707+1·0,707)/(1,3·0,95)=18,55
см3 ;
![]() 33,2(0,707+1·0,707)/(1,3·1,2)=30,0 см3
.
33,2(0,707+1·0,707)/(1,3·1,2)=30,0 см3
.
Требуемые размеры бруска обрешетки при n=1
![]() см .
см .
По сортаменту принимаем квадратный брусок 60х60 мм .
![]() .
.
Моменты инерции и моменты сопротивления обрешётки 125![]() 25(h)
25(h)
![]() ;
; ![]() ;
;
![]()
![]()
Проверка прочности в стадии эксплуатации даёт ![]() , что меньше
, что меньше ![]() =12,35
МПа.
=12,35
МПа.
Проверка жёсткости:
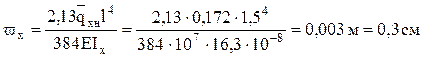 ;
;
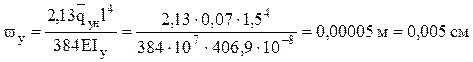 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.