Синтез эвольвентного зубчатого зацепления. Геометрические параметры зубчатых колес. Эвольвентные профили зубьев. Геометрия положительного зацепления

8. Синтез эвольвентного зубчатого зацепления

8.1. Основные положения

Зубчатой передачей называется трехзвенный механизм, в состав которого входят зубчатые звенья, имеющие выступы (зубья), передающие вращательное движение. Колесо с меньшим числом зубьев называют шестерней, ей присваивают индекс 1. Колесо с большим числом зубьев — колесо (индекс 2).

Боковые поверхности (профили) сопряженных зубьев должны удовлетворять основной теореме зацепления: для того, чтобы передаточное отношение было постоянным, общая нормаль к профилям в точке соприкасания должна пересекать межосевую линию в одной и той же точке, называемой полюсом зацепления.

Передаточное отношение зубчатого механизма равно взятому со своим знаком отношению числа зубьев колеса к числу зубьев шестерни – формула (2.2):

i₁₂ = ± z₂ /z₁.

Знак плюс относится к внутреннему зацеплению, минус – к внешнему. Эвольвентное зацепление соответствует основной теореме, обладая другими важными достоинствами:

а) высокая прочность; в силовых зубчатых передачах эвольвентное зацепление имеет преобладающее применение;

б)  технологичность, определяемая нарезанием инструментом с прямолинейными кромками высокопроизводительными методами обкатки;

в) постоянство передаточного отношения при работе колес с любыми числами зубьев;

г) нечувствительность к изменению межосевого расстояния; в эвольвентном зацеплении передаточное отношение не зависит от межосевого расстояния, так как может быть определено отношением основных диаметров, остающихся неизменными в любом зацеплении при любой точности сборки;

д) возможность изменения качественных показателей за счет смещения инструмента.

8.2. Геометрические параметры зубчатых колес

Соотношения между элементами колес установлены стандартом на исходный контур (ГОСТ 13755-81):

 a = 20⁰, где - коэффициент высоты головки зуба;  — коэффициент радиального зазора;  — коэффициент радиуса переходной кривой; a — угол профиля; это угол наклона профиля исходного контура к нормали к его средней линии.

Одним из основных параметров зацепления является модуль. Модуль — линейная величина, в  раз меньшая окружного шага зубьев.  Через модуль рассчитывают все геометрические параметры зубчатых колёс. Диаметры окружностей вершин, впадин, делительные и основные рассчитывают для зубчатого колеса. Для зубчатого зацепления также рассчитывают диаметры начальных окружностей. Геометрические параметры зубчатого колеса внешнего зацепления показаны на рис. 8.1.

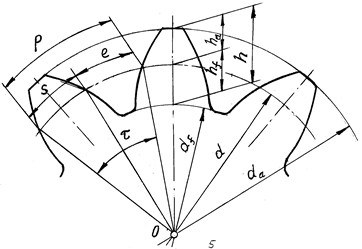
Рис. 8.1

       Делительной называется окружность, для которой модуль имеет стандарную величину. Делительный диаметр равен

d = mz.                                                      (8.1)

По делительной окружности шаг также будет стандартнымЯ. Шаг -  это расстояние, измеренное по дуге окружности между двумя одноименными профилями соседних зубьев. Величина шага

p = p m.                                                    (8.2)

         Основной называется окружность, служащая для образования эвольвенты. Эвольвенту описывает каждая точка прямой, перекатывающейся без скольжения по окружности. Основной диаметр равен:

d_b =2r_b =  d∙cosα =  mz∙cosα .                                          (8.3)

Высота головки зуба так же, как и некоторые другие параметры колеса, выражается произведением модуля на коэффициент, имеющий в верхнем индексе звездочку. Величина высоты головки:

.                                                    (8.4)

         Величина радиального зазора

.                                                    (8.5)

Высота ножки зуба больше высоты головки на величину радиального зазора:

.                                        (8.6)

Полная высота зуба = это сумма высот головки и ножки:

.                                   (8.7)

Диаметр вершин нулевого колеса определяется суммой делительного диаметра и двух высот головки зуба:

.                                  (8.8)

Диаметр впадин определяется разностью делительного диаметра и двух высот ножки зуба:

.                       (8.9)

Толщина зуба по делительной окружности обозначается через s. Ширина впадины — e. Для нулевого колеса

s = e = 0,5p = 0,5pm.                                    (8.10)

Угловой шаг колеса

t = 2p/z.                                               (8.11)

8.3 Эвольвентные профили зубьев

В общем случае эвольвента (рис. 8.2) описывается двумя уравнениями:

 = inv a = tga – a;                                       (8.12)

r = r_b/cosa,                                           (8.13)

где r – текущий радиус-вектор.

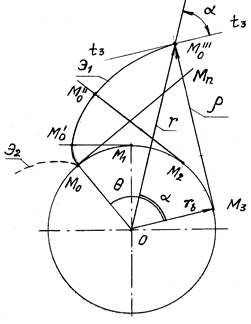
Рис. 8.2

Тригонометрическая функция tga – a называется инволютой (эвольвентной функцией). Таблица инволют приведена в прил. А.Острый угол a между касательной к эвольвенте и текущим радиусом-вектором, проведенным через точку касания, называется углом профиля (рис. 8.2). Угол, образованный начальным радиусом-вектором эвольвенты и ее текущим радиусом-вектором, называется эвольвентным углом и обозначается .

Угол профиля a_y по любой окружности диаметра d_y определяется по формуле:

a_y = arccos(d_b/d_y).                                         (8.14)