Синтез эвольвентного зубчатого зацепления. Геометрические параметры зубчатых колес. Эвольвентные профили зубьев. Геометрия положительного зацепления, страница 6

d_f2 = 4(41 – 2,5 +2·0,53) = 158,24 мм.

12. Делительные толщины зубьев — формула (8.17):

s₁ = 0,5·4 + 2·0,6·4·tg20º = 8,03 мм;

s₂ = 0,5·4 + 2·0,53·4·tg20º = 7,83 мм.

13. Углы профиля по вершинам и толщины зубьев по вершинам — формулы (8.28) и (8.29):

41,01º = 41º01´;

28,42º = 28º25´.

 0,15392; 0,014510.

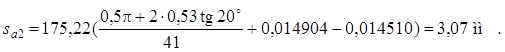
14. Передаточное отношение — формула (2.2):

i₁₂ = – 41/12 = – 3,41.

15. Коэффициент перекрытия — формула (14.57):

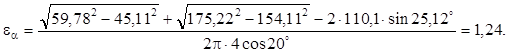
Выводы:

1. Толщина зуба шестерни больше минимально допускаемой s_aдоп = 0,25·4 = 1 мм.

2. Коэффициент перекрытия больше минимально допустимого (1,2).

8.9. Диаграммы удельных скольжений

Удельное скольжение равно отношению скорости скольжения профилей _s к тангенциальной составляющей скорости точки контакта ^t. Удельные скольжения шестерни и колеса рассчитывают по формулам:

;                                                 (8.33)

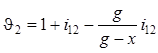,                                           (8.34)

где i₂₁ - передаточное отношение.

i₂₁ = 1/i₁₂ = z₁/z₂,                                        (8.35)

g — длина линии зацепления В₁В₂ (см. рис. 8.3);

g = a_w sin a_w;                                          (8.36)

х — расстояние, отсчитываемое от точки В₁; х_min = 0; х_max = g (рис. 8.6).

 

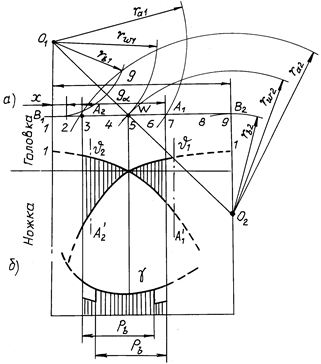
Рис. 8.6

В соответствии со свойствами эвольвенты расстояние х равно радиусу кривизны r₁ эвольвенты профиля шестерни в точке контакта. В этом случае радиус кривизны профиля колеса

r₂ = g – r₁.                                                (8.37)

В точках В₁ и В₂ диаграммы имеют ординаты 1 и –¥. Практически диаграммы реальны в пределах активной линии зацепления А₁А₂. За ее пределами диаграммы показаны штриховыми линиями.

Признаком оптимальной износостойкости является равенство суммарных ординат удельных скольжений в начале и конце зацепления. Из рис. 8.6, а следует, что износостойкость изображённого зацепления не будет оптимальной, так как в точке А₂  износ профилей будет больше, чем в точке А₁. Оптимальный результат может быть достигнут увеличением смещения шестерни с одновременным уменьшением смещения колеса (штрих-пунктирные линии на рис. 8.6).

8.10. Диаграмма коэффициента давления

Коэффициент давления учитывает влияние геометрии зубьев на величину контактных напряжений, возникающих в местах соприкосновения зубьев. Высокие контактные напряжения вызывают выкрашивание рабочей поверхности зубьев. Контактное напряжение определяют по формуле Герца:

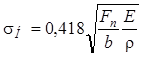,                                            (8.38)

где F_n — нормальное усилие, Н, приложено по нормали к эвольвентной поверхности зуба; b — ширина прямозубого колеса, мм; Е — приведенный модуль упругости, МПа; r — приведенный радиус кривизны, мм. Помножив и разделив на модуль m подкоренные выражения формулы (8.38), получают:

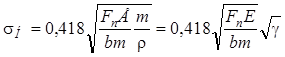,                            (8.39)

где g — коэффициент давления.

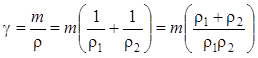.                                (8.40)

С учетом того, что при построении диаграмм r₁ = х, а r₂ = g – x, формула расчета g приобретет вид:

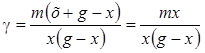.                                    (8.41)

Диаграмма коэффициента давления g приведена на рис. 8.6, б. Реальные очертания диаграмма имеет в пределах линии зацепления А₂А₁, причем в зонах двухпарного зацепления, определяемых размером основного шага r_b, откладываемого от точек А₂ и А₁ в пределах активной линии зацепления, ординаты делят пополам. Из диаграммы видно, что при однопарном зацеплении наименьшие контактные напряжения возникают вблизи полюса зацепления W и соответственно вблизи полюсной линии на поверхности зуба. Влияние смещения на контактную прочность зубчатой передачи может быть оценено по расчетной формуле:

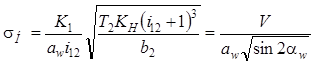,                       (8.42)

где K₁ — численный коэффициент; T₂ — вращающий момент на колесе, Н·мм; K_H — коэффициент нагрузки; b₂ — ширина венца колеса, мм; V — параметрический коэффициент, обобщающий все параметры, кроме a_w и .