Рычажный механизм поперечно-строгального станка

1 РЫЧАЖНЫЙ МЕХАНИЗМ ПОПЕРЕЧНО-СТРОГАЛЬНОГО СТАНКА

1.1  Структурный анализ

Цель структурного анализа – разложение рычажного механизма на структурные группы – группы Ассура. Группы Ассура – плоская кинематическая цепь с числом степеней свободы, равным нулю. Она содержит только низшие кинематические пары – вращательные и поступательные.

Число степеней свободы W определено по формуле Чебышева:

,                                              (1.1)

где  n - число подвижных звеньев, n = 5; p₁ - число низших кинематических пар,

p₁ = 7; p₂ - число высших кинематических пар, p₂ = 0.

Механизм имеет одно начальное звено.

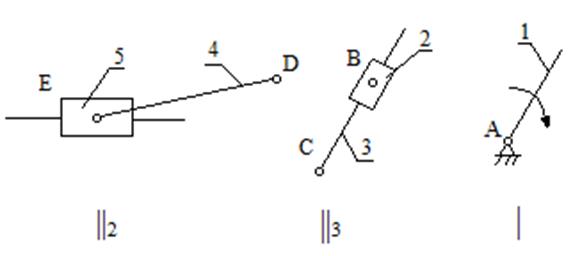
Рисунок 1.1 – Группы Ассура

Формула строения механизма:

I (1) – II₃ (2,3) – II₂ (4,5);

Механизм поперечно-строгального станка второго класса.

    1.2 Кинематический анализ

1.2.1 Планы положений

План положений - кинематическая схема механизма, выполненная в масштабе.

Масштаб плана положений μ_l определён из формулы, мм/м [1]:

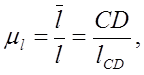                                             (1.2.1)

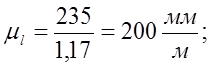
Длины отрезков, изображающих длины звеньев:

                         (1.2.2)

                                      (1.2.3)

                         (1.2.4)

                                        (1.2.5)

       (1.2.6)

       (1.2.7)

 Вычерчена окружность радиуса AB и разделена на 12 частей. Из точки А по вертикали вниз проведен y₁ и поставлена точка C, а по вертикали вверх проведен у₂ и проведена направляющая x-x. Из точки С через точку B проведена прямая CD. Из точки D проведена прямая DE так, что точка E оказалась на направляющей x-x.

1.2.2 Планы скоростей

Для построения плана скоростей составлена система векторных уравнений. Точка B кинематической схемы принадлежит трем звеньям. Точки B₁ и B₂ движутся как одно целое. Точка B₃ принадлежит кулисе 3 и меняет положение на звене в зависимости от угла поворота кривошипа. Кинематика точки B₃ и будет искомой:

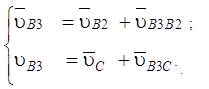                                      (1.2.8)

Линейная скорость:

_B1 = _B2 = w₁l_AB = 10×0,08 = 0,8 м/с.                     (1.2.9)

Масштаб плана скоростей:

 m = pb₁/_B1 = 60/0,08 = 75 мм/(м×с^-1).                  (1.2.10)

Из полюса p проведен вектор pb₁ = 60 мм перпендикулярно AB в сторону вращения. Из его конца проведено направление _B3B2 параллельно звену CD. Из полюса p (так как _C   = 0) проведено направление _B3C перпендикулярно CD до пересечения с направлением _B3B2. В искомую точку b₃ направлены стрелки искомых векторов.

Полученные длины отрезков:

pb₃ = 35мм;

b₃b₂ = 49 мм.

Положения точек d и s₃ найдены из пропорций:

pd = pb₃×CD/B₃C = 35×235/139 = 59,2 мм;

ps₃ = 0,5×59,2 = 29,6 мм.

Точка d получена на продолжении pb₃, точка s₃ — посередине pd.

Линейные скорости:

_B3 = pb₃/m = 35/75 = 0,47 м/с;                            (1.2.11)

_D = 60/75 = 0,8 м/с;                                   (1.2.12)

_S3 = 30/75 = 0,4 м/с;                                   (1.2.13)

_B3B2 = 49/75 = 0,65 м/с.                                  (1.2.14)

Угловая скорость кулисы:

          w₃ = _B3C/l_B3C = _B3/(B₃C/m_l) = 0,47/(139/200) = –0,67 с^-1.       (1.2.15)

Направление w₃ — по часовой стрелке.

Построен план скоростей диады 4–5. С диадой 2–3 ее связывает точка D, кинематика которой определена. Система векторных уравнений диады 4–5 аналогична (1.2.8):

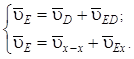                                             (1.2.16)

Из точки d проведено направление _ED перпендикулярно DE. Из полюса p проведено направление x–x до пересечения с направлением _ED в точке e.       Длины отрезков:

pe = 58,5 мм;

de = 5 мм.

Точку s₄ находим из пропорции ds₄ = 0,5de = 0,5×5 = 2,5 мм. Отрезок ps₄ = 59 мм.

Линейные скорости:

_E = 58,5/75 = 0,78 м/с;                                    (1.2.17)

          _ED = 5/75 = 0,07 м/с;                                    (1.2.18)

             _S4 = 59/75 = 0,79 м/с.                                             (1.2.19)

Угловая скорость шатуна w₄ = _ED/l_DE = 0,07/0,4 = –0,18 c^-1.         (1.2.20)

Направление w₄ — по часовой стрелке.

1.2.3 План ускорений

План ускорений построен также начиная с диады 2–3. Система векторных уравнений:

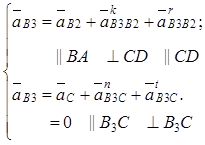                                                (1.2.21)

Нормальные ускорения  и  — центростремительные, направлены к центрам вращения А и С. Векторы, известные по величине и направлению:

          a_B1 = a_B2 = w₁²l_AB = 10²×0,08 = 8 м/с²;                    (1.2.22)

           = /l_B3C = 0,47²/(140/200) = 0,32 м/с².                  (1.2.23)

Направление кориолисова ускорения получено поворотом вектора относительно ускорения _B3B2 на 90^о в сторону w₃ (по часовой стрелке).

Его модуль:

           = 2w_3B3B2 = 2×0,67×0,65 = 0,87 м/с².                      (1.2.24)     

Масштаб плана ускорений m_a = pb₁/a_B1 = 160/8 = 20 мм/(м/с²). (1.2.25)