Другие предметы \ Теория механизмов и машин

Рычажный механизм поперечно-строгального станка, страница 2

Длины отрезков на плане ускорений:

b₁k = m_a = 0,87×20 = 17,4 мм;

pn₁ = m_a = 0,32×20 = 6,4 мм.

Из полюса p проведен вектор pb₁ = 160 мм параллельно AB к точке A. Из его конца перпендикулярно BC отложен отрезок b₁k = 17,4 мм, из конца которого проведено направление относительного ускорения параллельно звену CD. Решая второе уравнение системы, из полюса p отложен отрезок pn₁ = 6,4 мм параллельно звену CD к центру вращения C. Из конца отрезка pn₁проведено направление, перпендикулярное звену CD, до пересечения с направлением в точке b₃.

Полученные длины отрезков:

pb₃ = 112,5 мм;

n₁b₃ = 113 мм.

Точки d и s₄ найдены из пропорций:

pd = pb₃CD/B₃C = 112,5×235/139 = 190,2 мм;

ps₃ = 0,5×190,2 = 95,1 мм.

Линейные ускорения:

a_ВЗ = πb₃/μ_а = 112,5/20 = 5,6 м/с²; (1.2.26)

= n₁b₃/μ_а = 113/20 = 5,7 м/с²; (1.2.27)

a_D = πd/μ_а = 190,2/20 = 9,5 м/с²; (1.2.28)

a_S₃ = πs₃/μ_а = 95,1/20 = 4,8 м/с². (1.2.29)

Угловое ускорение кулисы:

= 5,7/(140/200) = –8,1 с^-2. (1.2.30)

Направление ε₃ — по часовой стрелке.

Для построения плана ускорений диады 4–5 составлена система векторных уравнений для диады 2-го вида:

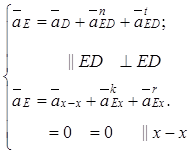(1.2.31)

Нормальная составляющая = /l_DE= 0,07²/0,4 = 0,01 м/с². (1.2.32)

Длина отрезка dn₂ = m_a = 0,01×20 = 0,2 мм. Из конца вектора pd отложен отрезок dn₂ = 0,2 мм параллельно ED в сторону точки D. Далее ему перпендикулярно проведено направление . Из полюса p проведено направление параллельно направляющей x–x. Точка пересечения направлений e определяет длины отрезков и величины векторов.

Полученные длины отрезков:

ps₄ = 192 мм;

n₂e = 2 мм;

pe = 192 мм.

Линейные ускорения:

a_E= 192/20 = 9,6 м/с²; (1.2.33)

a_S₄= 192/20 = 9,6 м/с²; (1.2.34)

= 2/20 = 0,1 м/с². (1.2.35)

Угловое ускорение шатуна:

e₄= /l_ED= 0,1/0,4 = 0,25 с^-2 (против часовой стрелки). (1.2.36)

1.2.4 Метод кинематических диаграмм

Метод кинематических диаграмм – графический метод кинематического анализа.

Диаграмма перемещений S_C = S_C (t) построена в масштабах µ_s и µ_t. На оси абсцисс отложено 12 равноотстоящих отрезков общей длиной = 240 мм. Масштаб времени, мм/c [1]:

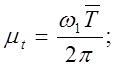(1.2.37)

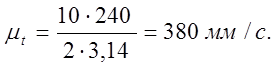
Первая точка диаграммы перемещений - точка 9, следующая - точка 10, т.к. кривошип вращается по часовой стрелке. Перемещение ползуна E отложено в масштабе: µ_S = µ_l. Максимальное перемещение поршня – это ход резца H=2l_AB.

Диаграмма скорости V_C = V_C(t) построена методом графического дифференцирования. На каждом участке диаграммы S_C = S_C(t) кривая заменена стягивающей прямой – хордой. P1 – полюс. P18 – отрезок дифференцирования, принят равным 40 мм. Из полюса P1 проведены лучи параллельные хордам кривой на графике S_C = S_C(t) до пересечения с осью ординат. Эти отрезки изображают скорость на середине соответствующего участка. На серединах всех участков про-ведены отрезки 9-10`, 9-11` и т.д. они соединены плавной кривой, эта кривая - диаграмма V_C = V_C(t). Масштаб диаграммы скоростей, мм/м·с^-1 [1]:

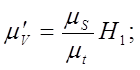(1.2.38)

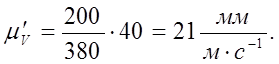
Аналогично выполнено повторное дифференцирование для построения диаграммы ускорений a_C = a_C(t) в масштабе, мм/м·с^-1 [1]:

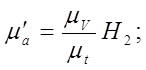(1.2.39)

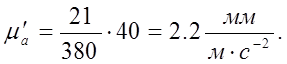
1.2.5 Аналитический метод кинематического анализа

Исходные данные:

угловая скорость кривошипа ω₁ =-10 рад/с;

длина звена АВ: l_AB = l₁ = 0,08 м;

длина звена CD l_CD = l₃ = 1,17 м; длина между точками A и C y₁ = l₄ = 0,65 м;

центр масс звена CD l_CS₃ = 0,5 l_CD = 0,59 м;

угол поворота кривошипа φ₁ = 60˚; шаг = 30˚.

Алгоритм расчёта кривошипно-кулисного механизма

Расчетная схема механизма представлена на рис. 1.2. Длины звеньев заменены векторами , и .

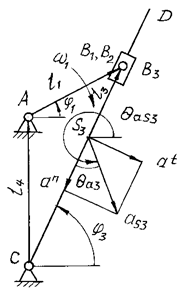
Рисунок 1.2 – Расчетная схема кривошипно-кулисного механизма

Особенностью механизма является то, что точка В принадлежит одновременно трем звеньям. Точка кривошипа В₁и точка В₂ камня кулисы имеют общую ось и одинаковые кинематические параметры. Точка В₃ на кулисе меняет свое положение в зависимости от координаты кривошипа. Ее кинематические параметры переменны.

Координата точки В₃:

(1.2.40)