Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей

1.Случайные события, вероятность, теоремы сложения и умножения вероятностей (примеры). Формула полной вероятности, формула Байеса (примеры). Случайные величины. Свойства интегральной функции и плотности распределения вероятностей (примеры).

Случайное событие – всякий факт, который в результате испытания может произойти или не произойти. События B₁,B₂,..B_n образуют полную группу событий, если хотя бы одно из них непременно должно произойти в ходе испытания. Полная система Ω попарно несовместимых равновозможных событий (такие события называют элементарными) называется пространством элементарных событий.

Система подмножеств V пространства элементарных событий называется алгеброй множеств, если выполнены следующие требования:

1., .

2. Из того, что  следует, что .

3. Из того, что  следует, что

 и .

Аксиоматика теории вероятностей (определение вероятности).

Аксиома 1.  Каждому случайному событию A поставлено в соответствие неотрицательное число p(A), называемое его вероятностью.

Аксиома 2.  p(Ω) = 1.

Аксиома 3. (аксиома сложения). Если события A₁,A₂..A_n попарно несовместимы, то p(A₁+A₂+..+A_n) = p(A₁)+p(A₂)+..+p(A_n).

Теорема сложения.

Если A и B – произвольные события, то справедлива формула:

p(A+B) = p(A) + p(B) – p(AB).

Теорема умножения.

Вероятность совместного наступления событий A и B равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло:

.

Положим, что событие B может осуществляться с одним и только одним из n несовместимых событий A_i (i = 1,2..n). Тогда справедлива формула полной вероятности:

Выведем теперь формулу Байеса, или, как еще говорят, формулу вероятности гипотез. Требуется найти вероятность события A_i, если известно, что B произошло. Согласно теореме умножения, имеем:

Отсюда:

Наконец, используя формулу полной вероятности, находим, что:

Это и есть формула Байеса. Общая схема применения этой формулы к решению практических задач такова. Пусть событие B может протекать в различных условиях, относительно характера которых может быть сделано n гипотез:A₁,A₂..A_n. По тем или иным причинам нам известны вероятности p(A_i) этих гипотез до испытания. Известно также, что гипотеза A_i сообщает событию B вероятность p(B/A_i). Произведен опыт, в котором событие B наступило. Это должно вызвать переоценку вероятностей гипотез A_i – формула Байеса количественно решает этот вопрос.

Случайной называется величина, которая в результате  опыта принимает то или иное возможное значение, заранее неизвестное и зависящее от случайных причин.

Функцией распределения вероятностей случайной величины X называется вероятность выполнения неравенства , рассматриваемая как функция аргумента x:

Функция распределения показывает, как зависит от величины выбранного уровня x вероятность того, что значения случайной величины X не превосходят этот уровень.

Свойства функции распределения:

1.

2. Функция распределения непрерывна справа.

3.

4.  и

5.

6. Функция распределения дискретной случайной величины есть ступенчатая (кусочно-постоянная функция).

7. Функция распределения непрерывной случайной величины непрерывна и дифференцируема.

Производная от функции распределения вероятностей называется плотностью распределения вероятностей:

Зная плотность распределения вероятностей, можно найти функцию распределения:

Основные свойства функции распределения:

1. ,

2.

3.

Функция распределения и плотность вероятности дают полную характеристику случайной величины.

2. Моменты СВ. Гауссовское и равномерное распределение случайных величин (примеры). Свойства ПРВ системы СВ. Статистически независимые СВ. Числовые характеристики СВ. Математическое ожидание. Дисперсия. Мода. Медиана.

Однако в ряде случаев о случайной величине достаточно иметь лишь некоторое общее представление. В теории вероятностей такое представление дают числовые характеристики случайных величин – моменты.

Начальный момент k-го порядка:

Для непрерывной случайной величины:

  в предположении, что этот интеграл сходится.

Для дискретной случайной величины:

Центральный момент k-го порядка:

Для непрерывной случайной величины:

Для дискретной случайной величины:

Плотность распределения вероятностей  равномерно распределенной случайной величины на отрезке [a,b] равна

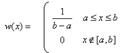
Плотность  вероятностей гауссовской (нормально распределенной) случайной величины имеет вид:

Нормальное распределение определяется двумя параметрами: математическим ожиданием m_x и дисперсией D_x. Математическое ожидание, характеризующее положение плотности распределения на числовой оси, для гауссовской случайной величины является наивероятнейшем значением.

Функцией распределения системы n случайных величин (X₁,X₂..X_n) называется вероятность совместного выполнения n неравенств , рассматриваемая как функция аргументов x_i:

Плотностью распределения вероятностей системы n непрерывных случайных величин (X₁,X₂,…X_n) называется смешенная производная n-го порядка функции распределения:

Свойства плотности распределения n случайных величин:

1.