Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 3

Случайным процессом X(t) называется функция неслучайного аргумента t (времени), значение которой при любом фиксированном является случайной величиной . Сечением случайного процесса в точке  называют случайную величину , соответствующую фиксированному моменту времени.

Классификация СП.

Все СП можно подразделить на:

1. Непрерывные – это СП, у которого область определения и область значений непрерывные множества.

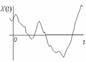
2. Дискретные СП – это СП, область определения которых непрерывное множество, а область значений – квантованное.

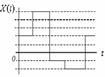
3. Случайная последовательность – область определения – дискретное множество, область значений – непрерывное множество.

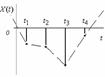
4. Дискретная случайная последовательность – область определения и область значений – дискретные множества.

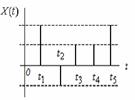
Одномерной функцией распределения СП X(t) называется функция двух аргументов:

где - вероятность того, что в момент времени t₁ случайная величина X(t₁) будет меньше некоторого уровня x₁.

Производная от этой функции по x₁ называется одномерной плотностью распределения вероятностей случайного процесса:

Математическим ожиданием СП X(t) называется неслучайная функция , значение которой при каждом фиксированном t равно математическому ожиданию соответствующего сечения СП:

Для непрерывного СП:

Для дискретной случайной последовательности

где - вероятность того, что в момент времени t_i случайная дискретная последовательность приняла значение x_k.

Свойства математического ожидания СП (- детерминированная функция):

1.

2.

3.

4. Для НСП

5. Для НСП

Дисперсией СП X(t) называется неслучайная неотрицательная функция , значение которой при каждом фиксированном t равно дисперсии соответствующего сечения случайног опроцесса X(t):

Свойства дисперсии СП:

1.

2.

3. Для НСП

4.ДляНСП

5. .

5. Ковариационная и нормированная корреляционная функции СП. Взаимная ковариационная функция СП.  Характеристики суммы СП.

Ковариационной функцией случайного процесса X(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна ковариационному моменту соответствующих сечений:

Для непрерывных СП:

Для дискретной случайной последовательности:

где - совместная вероятность того, что в момент времени t₁ случайная дискретная последовательность приняла значение , и в момент времени t₂ значение .

Свойства ковариационной функции СП:

1.

2.

3. Если , то

4.Если,то

5.

Корреляционной (автокорреляционной) функцией случайного процесса X(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна корреляционному моменту соответствующих сечений:

Связь между корреляционной и ковариационной функциями дается соотношением:

Нормированной корреляционной функцией случайного процесса X(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна коэффициенту корреляции соответствующих сечений:

Свойства нормированной корреляционной функции:

1.

2.

3.Если,то

4.Если,то

5.

Взаимной ковариационной функцией случайных процессов X(t) и Y(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна взаимному ковариационному моменту соответствующих сечений:

Свойства взаимной ковариационной функции:

1.

2.Еслии , то

3. Если  и , то

4. .

Взаимной корреляционной функцией случайных процессов X(t) и Y(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна взаимному корреляционному моменту соответствующих сечений:

Нормированной корреляционной функцией случайных процессов X(t) и Y(t) называется неслучайная функция двух аргументов , которая для каждой пары фиксированных значений t₁, t₂ равна нормированному взаимному корреляционному моменту соответствующих сечений:

.

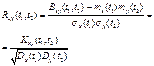6. Стационарные и стационарно связанные СП. Эргодические СП. Интервал корреляции.