Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 6

Ковариационная функция и спектральная плотность мощности белого шума равны:        

Ковариационная функция процесса на выходе каузальной ЛС в переходном режиме:

Приравнивая t₁ и t₂ ,получаем выражение для дисперсии:

 

Спектральная плотность мощности на выходе ЛС:

В установившемся режиме взаимная ковариационная функция процесса на выходе ЛС:

Очевидно, что для измерения импульсной характеристики можно использовать взаимную ковариационную функцию. Схема такого измерителя приведена на нижеследующем рисунке.

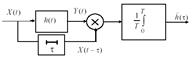
Найдем спектральные характеристики шума на выходе интегрирующей RC-цепочки (в установившемся режиме). Входной процесс – белый шум с математическим ожиданием .

Комплексная амплитудно-частотная и импульсная характеристики такой цепочки:

    

СПМ и КФ входного процесса имеют вид:

    

Перемножив СПМ входного процесса с квадратом амплитудно-частотной характеристики, имеем СПМ процесса на выходе:

Взяв преобразование Фурье от , получим ковариационную функцию процесса на выходе:

При воздействии белого шума RC-цепь выходной процесс имеет ковариационную функцию экспоненциального типа. Интервал корреляции равен постоянной времени цепи:

Дисперсия:.

14. Оптимальные линейные системы. Постановка задачи, модели, критерии. Основные этапы синтеза и анализа оптимальных систем.  Синтез согласованного фильтра.

Задача синтеза оптимальной линейной системы состоит в отыскании такой линейной системы, которая преобразовывала бы процесс с заданными характеристиками в процесс с требуемыми характеристиками. Статистический синтез оптимальных (наилучших) методов состоит в отыскании методов, которые обеспечивали бы наилучший (в некотором смысле) прием сигналов при наличии помех.

Прежде чем синтезировать систему, нужно располагать некоторой априорной информацией о вероятностных характеристиках как полезного сигнала, так и шума, и способ их взаимодействия. Априорная информация учитывается в виде математической модели:

1. Сигнал и помеха – СП: спектрально – корреляционные характеристики сигнала и помехи, распределения сигнала и помехи.

2. Детерминированный сигнал: характеристики сигнала: форма, длительность, частота и т.п.

Математические модели взаимодействия сигнала и помехи:

1. Аддитивная помеха: .

2. Мультипликативная помеха: .

3. Импульсная помеха:  с вероятностью p и  с вероятностью 1-p.

Для решения задачи статистического синтеза необходимо выбрать критерий оптимальности, на основании которого можно оценивать работу приемного устройства и по отношению к которому можно производить оптимизацию. Выбор критерия оптимальности непосредственно связан с характером решаемых задач. Наиболее распространенные критерии оптимальности:

1. Минимум среднеквадратической ошибки: .

2. Максимум отношения сигнал/шум: .

Этапы синтеза:

1. Анализ ОС.        

2. Точная или приближенная реализация.

Синтез согласованного фильтра.

Синтезируем фильтр по критерию (2).

Пусть входной сигнал имеет СПМ:

СПМ сигнала на выходе фильтра:

Взяв обратное преобразование Фурье от , получим сигнал на выходе фильтра. Его значение в момент времени  равна:

Дисперсия шума на выходе фильтра:

Отношение сигнал/шум на выходе фильтра в момент времени :

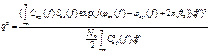
Для нахождения максимума этого выражения используем неравенство Буняковского-Шварца:

Выполнив необходимые преобразования в числителе с учетом неравенства, получим:

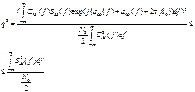
Это неравенство переходит в равенство при условии:

     

где  B – не равная нулю произвольная константа.

Такой фильтр называется согласованным, так как его амплитудно-частотная и фазочастотная характеристики согласованы с амплитудным и фазовым спектром сигнала.

15. Анализ согласованного фильтра. Согласованный фильтр как коррелятор. Плотность распределения вероятностей сигнала на выходе согласованного фильтра.

Выходной сигнал находится как пр. Фурье:

Выходной сигнал в момент времени равен:

С другой стороны сигнал на выходе согласованного фильтра:

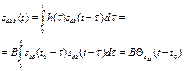
где - корреляционная функция сигнала: