Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 8

Оценка и образующий ее фильтр называются некаузальными, если для получения оценки используются все входные данные . Если для получения оценки используются прошлые данные, то фильтр называется каузальным.

Произвольную импульсную характеристику системы можно представить в виде:

Тогда СКО:

При отличном от нуля СКО больше, чем при . Поэтому производная от СКО по параметру  должна равняться нулю в точке . Воспользовавшись этим, получаем уравнение Винера-Хопфа:

Взяв преобразование Фурье от левой и правой, представляющей собой интеграл свертки, частей этого интегрального уравнения, получим:

    где - комплексная частотная характеристика фильтра Винера. На этом синтез фильтра Винера завершен.

Если оцениваемый процесс X(t) и шум N(t) являются некоррелированными и :

Тогда соответствующие спектральные плотности мощности имеют вид:

Получаем комплексную частотную характеристику:

 

Пример синтеза фильтра Винера:

Пусть имеется аддитивная смесь процессов с ковариационными функциями:

СПМ сигнала и помехи соответственно равны:

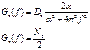
Введем безразмерный коэффициент , имеющий физический смысл отношения сигнал/шум в эффективной полосе частот. Эффективная полоса спектра сообщения X(t) равна:

Тогда дисперсия шума в эффективной полосе частот:

     откуда 

.

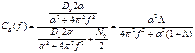19. Помехоустойчивая оценка линейно искаженных СП. Инверсный фильтр. Фильтр Винера. Пример синтеза фильтра Винера для оценки линейно искаженных СП.

В некоторых радиотехнических системах сигнал искажается не только шумом, но и линейной системой с известной импульсной характеристикой. Пусть наблюдаемый процесс:

 где - импульсная характеристика линейной искажающей системы.

Оцениваемый процесс X(t) и шум N(t) являются некоррелированными СП с известными спектральными плотностями мощности  и .

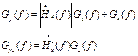
В этом случае комплексная частотная характеристика и минимальная среднеквадратическая ошибка соответственно равны:

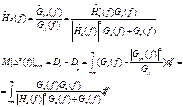
При отсутствии шума () фильтр Винера вырождается в так называемый инверсный фильтр

Инверсный фильтр, по сути, является обратным оператором по отношению к искажающему фильтру .

Пример синтеза фильтра Винера для оценки линейно искаженных СП.

Предположим, что наблюдаемый сигнал

где дифференцируемый оцениваемый процесс X(t) и белый шум N(t) являются некоррелированными взаимно стационарными случайными процессами с известными СПМ  и .

Если для оценки использовать инверсный фильтр, который в данном случае будет идеальным интегратором, то

Отсюда следует, что непосредственное интегрирование наблюдаемого сигнала Y(t) приведет к тому, что дисперсия шума на выходе интегратора, а, следовательно, и среднеквадратическая ошибка оценивания будут бесконечно большими. Это объясняется тем, что при     .

Комплексная частотная характеристика дифференциатора:

Тогда комплексная частотная характеристика фильтра Винера:

В отличие от инверсного фильтра фильтр Винера обеспечивает конечность ошибки оценивания.

20. Задача обнаружения сигналов. Наблюдаемая выборка. Гипотезы. Пространство наблюдений. Принимаемые решения. Ошибки.

Наблюдаемая реализация процесса Y(t) на входе приемного устройства, зависящая от состояния источника сигнала, взятая на конечном отрезке времени, называется выборкой:.

Задача обнаружения сигнала на фоне помех состоит в отыскании алгоритма обработки , при помощи которого выносится решение о наличии или отсутствии в ней сигнала.

Приемное устройство является не аналоговым, а цифровым. Поэтому непрерывная реализация y(t)  подвергается временной дискретизации. В этом случае наблюдение представляется конечномерным вектором: , здесь n – объем выборки.

Статистической гипотезой называется предположение о параметрах или виде распределения наблюдаемой реализации y(t). Выдвигается две гипотезы: H₀ и H₁, т.е. задача обнаружения – бинарная.

H₀:  - нулевая гипотеза (гипотеза).

H₁:  - альтернативная гипотеза (альтернатива). Здесь  - оператор, определяющий вид взаимодействия сигнала  и помехи , определяемый свойствами канала.