Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 4

СП X(t) называется строго стационарным или стационарным в узком смысле, если его плотность распределения вероятностей произвольного порядка n не меняется при любом сдвиге всей группы сечений  вдоль оси времени:

Свойства ССП:

1.

2.

3.

4.,и .

СП X(t) называется стационарным в широком смысле, если выполняются условия: и .

Два стационарных случайных процесса X(t) и Y(t) называются стационарно связанными, если их взаимная ковариационная функция зависит только от разности аргументов:

Свойства ССП:

1.

2.

ССП называется эргодическим в строгом смысле, если с вероятностью единица усреднение по всей совокупности реализаций дает тот же результат, что и усреднение по времени.

Достаточное условие эргодичности:

Интервалом корреляции называют минимальное расстояние между сечениями, при котором их можно считать практически некоррелированными. Интервал корреляции можно определить двумя способами:

1.

2. В этом случае интервал корреляции  определяется долей  от максимального значения нормированной корреляционной функции (). Решают уравнение: .

7. Спектральный анализ стационарных в широком смысле случайных процессов. Теорема Винера-Хинчина. Свойства СПМ.

Прямой перенос методов спектрального анализа детерминированных сигналов в теорию случайных процессов невозможен, так как интеграл Фурье от реализации случайного процесса, наблюдаемого на бесконечном интервале времени, расходится.  Это связано с тем, что при конечной средней мощности СП обладает бесконечной энергией.

Кроме того, амплитудный и фазовый спектры реализаций одного и того же СП будут отличаться друг от друга, так как они однозначно связаны с формой конкретной реализации СП. Для преодоления этих трудностей используется усреднение спектральных разложений.

Пусть x(t) – реализация ССП X(t). Спектральная плотность усеченной реализации:

Энергия усеченной реализации:

В соответствии с теоремой Парсеваля:

Средняя мощность реализации:

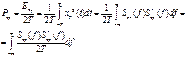
 - распределение мощности по частоте для усеченной реализации.

Спектральная плотность мощности:

Отсюда следует теорема Винера-Хинчина:

Спектральная плотность мощности и корреляционная функция ССП связаны между собой парой преобразований Фурье:

 и .

Используя тот факт, что , получим

Свойства СПМ:

1.

2.

3.   и 

4. Если , то  - для некоррелированных СП.

5.

6.

7. Если , то

8. Эффективная ширина спектра ее связь с интервалом корреляции СП. Соотношение неопределенности.  Взаимная СПМ двух стационарно связанных СП. Гауссовский СП и его свойства.

Эффективная ширина спектра определятся следующим образом:

Эту величину можно трактовать как ширину прямоугольной спектральной плотности мощности эквивалентного процесса, которая равна  в полосе частот  при равных дисперсиях обоих процессов.

Интервал корреляции, по определению:

Таким образом, связь между эффективной шириной спектра и интервалом корреляции:

Для процесса с любой ковариационной функцией справедливо неравенство (соотношение неопределенности):

Аналогично спектральной плотности мощности  определяется взаимная спектральная плотность мощности двух стационарно связанных СП X(t) и Y(t):

Случайный процесс называется гауссовским, если для любого конечного множества моментов времени  совокупности сечений   имеют совместную гауссовскую плотность распределения вероятностей:

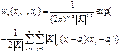
где  - математическое ожидание СВ , ;  - алгебраическое дополнение элемента  в детерминанте  матрицы ковариаций

в которой  представляет собой ковариационный момент , вычисленный для СВ  и .

Свойства гауссовского СП:

1. Гауссовский стационарный СП полностью определяется математическим ожиданием  и ковариационной функцией , так как в выражение плотности распределения вероятностей входят только эти величины.

2. Для гауссовского процесса некоррелированность сечений означает их статистическую независимость.

3. Из стационарности в широком смысле гауссовского СП следует его строгая стационарность, т.к. n-мерная плотность распределения вероятностей зависит только от разности отсчетов  и не изменится при любом сдвиге всей группы точек  вдоль оси времени на постоянную величину.