Несмещённость: Оценка ![]() называется несмещенной оценкой параметра
θ, если ее математическое ожидание равно истинному значению оцениваемого
параметра:
называется несмещенной оценкой параметра
θ, если ее математическое ожидание равно истинному значению оцениваемого
параметра: ![]() Смещение:
Смещение:![]()
Математическое ожидание смещения несмещенной оценки равно 0:
![]()
Состоятельность:
Оценка
![]() называется состоятельной оценкой параметра
θ , если
называется состоятельной оценкой параметра
θ , если ![]() сходится по вероятности к θ:
сходится по вероятности к θ:![]() δ>0
δ>0
Теорема:
Если
![]() и
и ![]() , то
, то ![]() состоятельная оценка параметра θ.
состоятельная оценка параметра θ.
Эффективность:
Оценка, удовлетворяющая неравенству Крамера-Рао, называется эффективной.Неравенство Крамера-Рао:
![]()
Здесь
![]() - информация по
Фишеру, содержащаяся в выборке объема n относительно неизвестного
параметра.
- информация по
Фишеру, содержащаяся в выборке объема n относительно неизвестного
параметра.
Для независимых выборочных значений
![]()
![]()
Мерой точности несмещенной оценки считают ее дисперсию:
![]() .
.
Для любой неэффективной оценки
![]() .
.
Оценка математического ожидания СП
Выборочное среднее:
![]()
Свойства выборочного среднего:
1. Выборочное среднее является несмещенной оценкой математического ожидания СП:
![]()
Дисперсия выборочного среднего:
![]()
2. Выборочное среднее является состоятельной оценкой математического ожидания СП, т.к.
![]()
Относительная ошибка оценки математического ожидания СП:
![]()
Вопрос 28
Оценка дисперсии СП при известном и неизвестном математическом ожидании. Оценка вероятности превышения СП порога
Оценка дисперсии СП при известном и неизвестном математическом ожидании
МО СП известно: Выборочная дисперсия:
![]()
Выборочная дисперсия является несмещенной оценкой дисперсии СП при известном его математическом ожидании
![]()
МО СП неизвестно: Выборочная дисперсия:
![]()
Выборочная дисперсия является смещенной оценкой дисперсии СП при неизвестном его математическом ожидании.
![]()
![]()
Оценка дисперсии СП:
![]()
Оценка вероятности превышения СП порога
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Свойства частоты:
1.Частота является несмещенной оценкой вероятности превышения порога СП:
![]()
Дисперсия частоты:
![]()
2. Частота является состоятельной оценкой вероятности превышения порога СП, т.к.
![]()
![]()
Относительная ошибка оценки вероятности превышения порога СП:
![]()
![]()
Вопрос 30. МП оценки. МП оценка математического ожидания гауссовского СП. МП оценка постоянной величины при неравноточных измерениях
Оценка максимального правдоподобия используется для оценки неслучайных параметров, т.е. когда отсутствует или не задано априорного распределение w(θ) оцениваемого параметра θ.
![]()
Здесь
Ly(θ)
– функция правдоподобия (функция неизвестного параметра θ при фиксированных
значениях ![]() .
.
Для выборки из независимых отсчётов уравнение правдоподобия:
![]()
![]()
МП оценка математического ожидания гауссовского СП:
Плотность распределения вероятности гауссовского СП:
![]()
![]()
Следовательно,
![]()
Поэтому,
![]()
выборочное среднее является МП оценкой МО гауссовского СП.
МП оценка постоянной величины при неравноточных измерениях
Пусть некоторая величина измеряется неравноточными приборами, которые осуществляют измерения без систематических ошибок, но с разными дисперсиями. Ошибка измерения подчиняется гауссовской ПРВ. Ошибки статистически независимые от измерения к измерению. Каждым прибором проводится n измерений. Найти результирующую оценку параметра и дисперсию оценки.
Первый прибор:
![]()
Второй прибор:
![]()
Для измерения одним прибором
![]()
МП оценка:
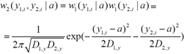
![]()
![]()
![]()
![]()
![]()
МАВ оценка математического ожидания гауссовского СП
МАВ – максимум апостериорной вероятности.
В качестве оценки параметра по наблюдаемой выборке принимается такое значение, при котором апостериорная ПРВ достигает максимума. Полагается, что оцениваемый параметр является случайной величиной с известной ПРВ w(θ).
![]()
- апостериорная ПРВ оцениваемого
случайного параметра θ при фиксированных значениях ![]() .
.
По формуле Байеса
![]()
![]()
![]()
Следовательно,
![]()
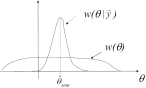
![]() (Для МП оценки это может не выполняться)
(Для МП оценки это может не выполняться)
МАВ оценка математического ожидания гауссовского СП:
Априорное распределение:
Оценка по априорным данным
![]()
МП оценка
![]()
МАВ оценка:
![]()
![]()
![]()
![]()
![]()
![]()
Выводы:
1. МАВ оценка представляет собой взвешенную сумма МП оценки и оценки по априорным данным.
2. Точность МАВ оценки всегда не хуже МП оценки.
3.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.