Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 9

Совокупность всех реализаций СП Y(t) называется пространством наблюдения.

При решении бинарной задачи обнаружения возможны четыре случайных события:

1. Принято решение  об отсутствии сигнала при условии, что верна гипотеза H₁ – ошибка второго рода или пропуск сигнала.

2. Принято решение  о присутствии сигнала при условии, что верна гипотеза  H₁ – правильное обнаружение.

3. Принято решение  о присутствии сигнала при условии, что верна гипотеза  H₀  - ошибка первого рода или ложная тревога.

4. Принято решение  о присутствии сигнала при условии, что верна гипотеза  H₀ – правильное необнаружение.

Перечисленным событиям соответствуют условные вероятности:

1.

2.

3.

4.  .

Алгоритм обнаружения задает правило разбиения всего пространства наблюдений на две непересекающиеся области G₀ и G₁ , при которых полагаются истинными соответственно гипотезы H₀ и H₁. Поскольку пространство наблюдений разбивается на две непересекающиеся области, то для построения алгоритма обнаружения достаточно выбрать область G₀. Оптимальный алгоритм обнаружения устанавливает наилучший выбор области G₀ в рамках выбранного критерия.

21. Обнаружение сигналов. Критерий Байеса. Критерий МАВ. Критерии МП и Неймана-Пирсона.

Задача обнаружения сигнала на фоне помех состоит в отыскании алгоритма обработки наблюдаемой реализации на входе приемного устройства, при помощи которого выносится решение о наличии или отсутствии в ней сигнала.

Алгоритм обнаружения задает правило разбиения всего пространства наблюдений на две непересекающиеся области G₀ и G₁ , при которых полагаются истинными соответственно гипотезы H₀ и H₁. Поскольку пространство наблюдений разбивается на две непересекающиеся области, то для построения алгоритма обнаружения достаточно выбрать область G₀.

Критерий Байеса.

Для обнаружителей по критерию Байеса предполагаются известными априорные вероятности гипотез  и . Каждому из четырех возможных событий назначена некоторая стоимость: , , , . При этом выполняются условия:  и .

Если истинной является гипотеза H₀,то потери составят

В противном случае

где  и  - условные риски (условные потери). Средний риск (средние потери):

 Оптимальным Байесовским алгоритмом обнаружения сигнала считается такой выбор области G₀, при котором средний риск будет минимален

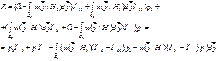Это выражение достигнет минимума, если подынтегральное выражение будет положительным.

Отношение правдоподобия:

Байесовский порог:

Критерий максимума апостериорной вероятности.

Условные вероятности гипотез при заданной выборке :

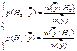
- апостериорные вероятности гипотез

При фиксированной выборке  истинной следует выбирать ту гипотезу, для которой апостериорная вероятность выше:

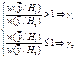
Критерий максимального правдоподобия.

При фиксированной выборке  истинной следует выбирать ту гипотезу, для которой функция правдоподобия выше:

Критерий Неймана-Пирсона.

Оптимальным алгоритмом является критерий, обеспечивающий минимум вероятности пропуска цели  при заданной вероятности ложной тревоги.

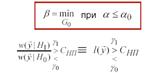
Порог выбирается из условия:

Вопрос 22 Синтез и анализ обнаружителя дискретного сигнала, наблюдаемого на фоне аддитивного гауссовского шума с некоррелированными отсчетами

 -мультипликативный гауссовский шум с независимыми отсчетами, нулевым математическим ожиданием и единичной дисперсией.

Найти алгоритм обнаружения

Решение:

 

Следовательно,

 

Отношение правдоподобия:

Логарифм отношения правдоподобия

Оптимальный алгоритм обнаружения сигналов

Приведённый порог:

Вопрос 27 Оценивание параметров СП. Несмещенные, состоятельные и эффективные оценки.  Неравенство Крамера-Рао. Оценка математического ожидания СП

Оценивание параметров СП

Точечной оценкой  неизвестного параметра называется приближенное значение этого параметра, полученного по выборке :

n – объём выборки

Свойства, которым должна удовлетворять оценка:

• состоятельность;• несмещенность;• эффективность.

Несмещенные, состоятельные и эффективные оценки