Случайные события, вероятность, теоремы сложения и умножения вероятностей. Формула полной вероятности, формула Байеса. Случайные величины. Свойства интегральной функции и плотности распределения вероятностей, страница 7

    

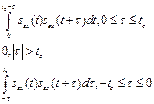
СПМ шума на выходе:

Следовательно, ковариационная функция шума:

с точностью до постоянного множителя совпадает с корреляционной функцией сигнала.

Приравняв к нулю, получим дисперсию шума на выходе фильтра:

Отсюда, отношение сигнал/шум:

Если на вход фильтра, согласованного с  подать любой другой сигнал , то выходной сигнал будет равен взаимной корреляционной функции этих сигналов:

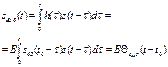Таким образом, согласованный фильтр вырабатывает на своем выходе взаимную корреляционную функцию, и, следовательно, может быть заменен коррелятором.

Найдем плотность распределения вероятностей на выходе согласованного фильтра в момент времени . Согласованный фильтр является фильтром нижних частот, в котором происходит нормализация белого шума, т.е. плотность распределения вероятностей на выходе СФ является гауссовской. Поэтому достаточно определить математическое ожидание и дисперсию выходного процесса:

Таким образом, имеем:

16. Оптимальный  и квазиоптимальный фильтры для видеоимпульса, наблюдаемого на фоне аддитивного белого шума.

Прямоугольный видеоимпульс задается следующим выражением:

 

Примем задержку пика выходного сигнала равной длительности входного сигнала: . Поскольку сигнал является симметричным относительно  , его импульсная характеристика будет с точностью до константы совпадать с сигналом:

Структурная схема согласованного фильтра с такой импульсной характеристикой приведена на нижеследующем рисунке:

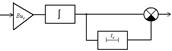
Энергия входного сигнала:

ОСШ на выходе фильтра:

Структурная схема физически осуществимого фильтра содержит идеальный интегратор и линию задержки, поэтому практическая реализация такого фильтра возможна лишь в той мере, в какой характеристики реальный элементов можно приблизить к идеальным. В ряде случаев удается получить квазиоптимальные фильтры с существенно более простой реализацией, эффективность которых близка к оптимальному согласованному фильтру.

Фильтр, согласованный с видеоимпульсом является фильтром нижних частот. Поэтому, в качестве квазиоптимального фильтра можно использовать интегрирующую RC-цепочку.

Сигнал на выходе интегрирующей RC-цепи при действии на ее вход прямоугольного импульса:

Максимум полезного сигнала на выходе фильтра достигается при . Максимальное значение выходного сигнала:

Дисперсия шума на выходе RC-цепи:

ОСШ:

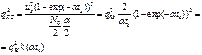Функция  достигает максимума при , т.е. оптимальное значение постоянной времени RC-цепи:

При этом проигрыш в отношении сигнал/шум:

.

17. Согласованная фильтрация при небелом шуме.

Пусть СПМ аддитивного шума  не постоянна во всей полосе частот, т.е. - окрашенный шум. Для построения согласованного фильтра воспользуемся методом «выбеливающего» фильтра. Выбеливающий линейный фильтр преобразует окрашенный шум  в белый  шум. Реакцию такого фильтра на сигнал  можно представить в виде:

 представляет собой аддитивную смесь детерминированного сигнала и белого шума. Фильтр, согласованный с  имеет комплексную частотную характеристику:

Квадрат амплитудно-частотной характеристики выбеливающего фильтра должен удовлетворять условию:

откуда

Спектральная плотность сигнала на выходе выбеливающего фильтра:

Тогда комплексная частотная характеристика для согласованного фильтра:

Комплексная частотная характеристика всего фильтра:

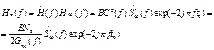
При этом ОСШ:  где     - энергия сигнала на выходе выбеливающего фильтра.

18. Синтез фильтра Винера (общий случай). Синтез фильтра Винера при некоррелированных сигнале и аддитивной помехе. Примеры синтеза фильтра Винера.

На вход фильтра поступает наблюдаемый на бесконечном временном интервале сигнал:

- оператор, определяющий способ взаимодействия сообщения и помехи. Последние считаются стационарно связанными случайными процессами с нулевым математическим ожиданием. Задача заключается в том, чтобы синтезировать линейный стационарный фильтр, формирующий оценку   СП , которая обеспечивает минимум СКО оценивания. В данном случае различаются спектрально-корреляционные характеристики сообщения и помехи.