ДОМАШНЕЕ ЗАДАНИЕ
Вариант №1
Исходные данные:
![]()
1. Рассчитайте параметры сигнала и шума, при которых
полученное на выходе СФ ОСШ ![]() ,
,
ОСШ согласованного фильтра:
|
|
|
|
![]()
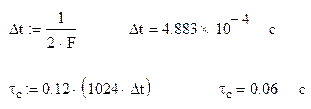
- интервал дискретизации
- длительность сигнала
Возьмём величину уровня сигнала: U=5 B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Рассчитаете зависимость ОСШ на выходе квазиоптимального фильтра от постоянной времени интегрирующего звена первого порядка
|
|
|
оптимальное значение постоянной времени интегрирующей RC-цепи |
|
|
Максимальное значение ОСШ при:
|
|
|
|
При этом значении ОСШ будет равно:
![]()
Проигрыш в сравнении с СФ:
|
|
3) Рассчитайте
длину реализации ![]() , при которой относительная
ошибка измерения дисперсии шума на выходе СФ не превышает 3%.
, при которой относительная
ошибка измерения дисперсии шума на выходе СФ не превышает 3%.
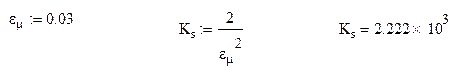
Отсчеты шума до фильтра были некоррелированы, после
прохождения через фильтр коррелированность отсчетов увеличивается, интервал
корреляции определяется АКФ входного сигнала, и корреляционная функция шума
будет равна нулю при ![]()
|
|
|
|
|
|
|
|
ближайшее кратное 1024 значение.
|
|
ЛАБОРАТОРНОЕ ЗАДАНИЕ
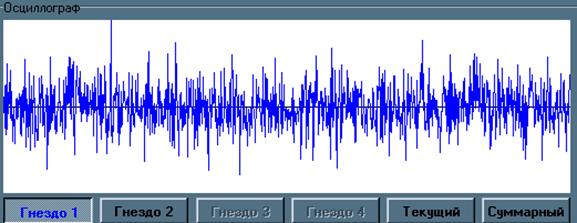
1. Включите генератор прямоугольного видеоимпульса; наблюдайте осциллограмму, измерьте параметры сигнала. Включите генератор шума, наблюдайте осциллограмму смеси сигнала и шума при различных уровнях последнего.
Сигнал: Uc=5 B, tc=0.06с
Смесь сигнала с шумом D=533.333
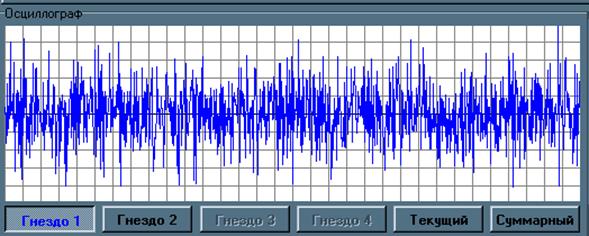
Смесь сигнала с шумом D=13.333
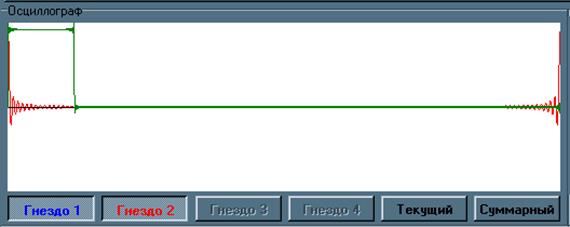
2. Получите импульсную и амплитудно-частотную характеристики согласованного фильтра и зафиксируйте их в отчете.
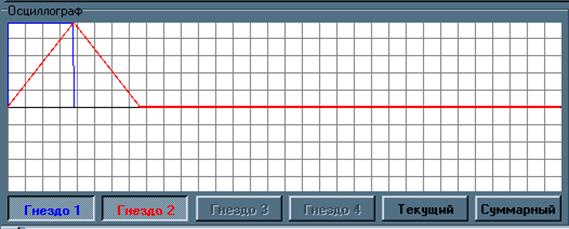
3. Получите автокорреляционную функцию сигнала и зафиксируйте ее в отчете.
4. Установите рассчитанные в домашнем задании параметры и экспериментально определите ОСШ на выходе СФ. Сравните с расчетом.
Уровень сигнала U=0.298 B на выходе
D(sum)=0.0157
![]()
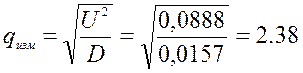
![]()
Относительная ошибка измерения: ![]() -
не выходит за пределы допустимой погрешности 3%.
-
не выходит за пределы допустимой погрешности 3%.
5. В качестве квазиоптимального фильтра включите интегрирующее звено первого порядка. Изменяя его постоянную времени, экспериментально определите ее оптимальное значение, обеспечивающее максимальное ОСШ.
Сначала установим расчетное τ=0,048
Уровень сигнала U=3,55040 B на выходе
D(sum)=2,732174
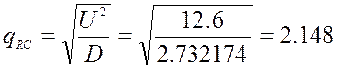
![]() =2,166
–расчетное ОСШ
=2,166
–расчетное ОСШ
Сравнивая полученные 2 значения,
можно сказать что относительная ошибка не превышает допустимой и равна ![]()
установим τ=0,054
Уровень сигнала U=3,36040 B на выходе
D(sum)=2,464372
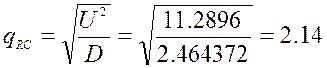
установим τ=0,062
Уровень сигнала U=3,083 B на выходе
D(sum)=2,098
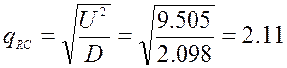
установим τ=0,042
Уровень сигнала U=3,7859 B на выходе
D(sum)=3,19
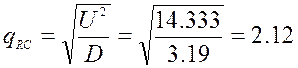
установим τ=0,036
Уровень сигнала U=3,56 B на выходе
D(sum)=4,04
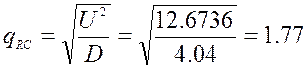
Нанесем полученные точки на теоретическую зависимость:
|
|
При сравнении, видно что кривые имеют схожий характер. Мы экспериментально доказали, что кривая зависимости ОСШ от постоянной цепи имеет максимум, и он совпадает теоретическим расчетом в пределах допустимой погрешности.
Проигрыш RC цепи по сравнению с согласованным фильтром:
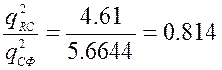 - это примерно 20%
- это примерно 20%
6. Используя ФНЧ с прямоугольной АЧХ в качестве квазиоптимального фильтра, исследуйте его эффективность в соответствии с заданием п.5.
fопт=1/tс=16,67 –оптимальная расчетная частота.
Установим частоту: f=16,7 при этом q = 1.96
f=25.6при этом q = 1.45
f=13 при этом q = 2.16
f=12.8 при этом q = 2.02
f= 6.4 при этом q =1.93
Получилось, что максимум
находится левее, чем расчетный. Это можно объяснить, тем что при расчете мы
описывали ФНЧ с АЧХ функцией вида 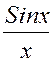 , а в программе он
идеальный с П- образной АЧХ, из-за этого максимум смещен влево.
, а в программе он
идеальный с П- образной АЧХ, из-за этого максимум смещен влево.
Проигрыш ФНЧ по сравнению с СФ:
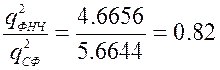
ВЫВОД:
СФ максимизирует ОСШ – это оптимальный фильтр, из-за того что он полностью согласован с сигналом, однако при построении СФ в схеме используются идеальные элементы(интегратор и линия задержки) поэтому на практике возможность добиться таких результатов существует лишь в той мере в какой характеристики реальных элементов можно приблизить к идеальным.
Проще строятся так называемые квазиоптимальные фильтры. В лабораторной работе использовались 2 фильтра(RC- цепь и ФНЧ с П-образной АЧХ) в качестве квазиоптимальных. В результате можно сделать вывод, что они могут заменить СФ, так как их эффективность не ниже, чем на 20 % по сравнению с СФ.
Министерство Образования и Науки Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра ТОР
Лабораторная работа № 2
«СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ»
Факультет: РЭФ
Группа: РТС9-72
Студент: Матохина Е.Б.
Преподаватель:
Гребенщиков К.Д.
Новосибирск, 2010г
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.