|
№ варианта |
Задача № 1 |
Задача № 2 |
Задача № 3 |
|
1. |
1 |
27. |
57 a |
|
2. |
2 |
28. |
57 b |
|
3. |
3 |
29. |
57 c |
|
4. |
4 |
30. |
57 d |
|
5. |
5 |
31. |
57 e |
|
6. |
6 |
32. |
57 f |
|
7. |
7 |
33. |
57 g |
|
8. |
8 |
34. |
57 h |
|
9. |
9 |
35. |
58 |
|
10. |
10 |
36. |
59 |
|
11. |
11 |
37. |
60 |
|
12. |
12 |
38. |
61 |
|
13. |
13 |
39. |
62 |
|
14. |
14 |
40. |
63 |
|
15. |
15 |
41. |
64 |
|
16. |
16 |
42. |
65 |
|
17. |
17 |
43. |
57 a |
|
18. |
18 |
44. |
57 b |
|
19. |
19 |
45. |
57 c |
|
20. |
20 |
46. |
57 d |
|
21. |
21 |
47. |
57 e |
|
22. |
22 |
48. |
57 f |
|
23. |
23 |
49. |
57 g |
|
24. |
24 а |
50. |
57 h |
|
25. |
24 б |
51. |
58 |
|
26. |
24 в |
52. |
59 |
|
27. |
24 г |
53. |
60 |
|
28. |
24 д |
54. |
61 |
|
29. |
25 |
55. |
62 |
|
30. |
26 |
56. |
63 |
1. Случайный процесс ![]() , где
, где ![]() –
случайная величина, равномерно распределенная на интервале
–
случайная величина, равномерно распределенная на интервале ![]() . Найти реализации случайного процесса,
наблюдаемые в результате двух опытов, в которых случайная величина
. Найти реализации случайного процесса,
наблюдаемые в результате двух опытов, в которых случайная величина ![]() приняла следующие значения:
приняла следующие значения: ![]() ,
, ![]() .
.
2. Найти трехмерную плотность распределения вероятностей случайного процесса с независимыми сечениями, одномерное распределение которого подчиняется рэлеевскому распределению экспоненциальному распределению.
3. Найти n-мерную плотность распределения вероятностей случайного процесса с независимыми сечениями, одномерное распределение которого подчиняется экспоненциальному распределению.
4. Одномерная плотность распределения
вероятностей случайного процесса ![]() имеет вид
имеет вид
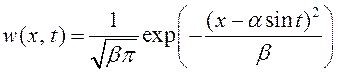 , где
, где ![]() и
и
![]() – неслучайные величины, причем
– неслучайные величины, причем ![]() . Определить математическое ожидание и дисперсию случайного
процесса
. Определить математическое ожидание и дисперсию случайного
процесса ![]() . Определить
вероятность выполнения неравенства
. Определить
вероятность выполнения неравенства ![]() .
.
5. Найти ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() и плотность распределения
вероятностей случайного процесса
и плотность распределения
вероятностей случайного процесса ![]() , где
, где ![]() – гауссовская случайная величина с
параметрами
– гауссовская случайная величина с
параметрами ![]() и
и ![]() ,
, ![]() и
и ![]() –
неслучайные величины.
–
неслучайные величины.
6. Найти ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() и функцию распределения вероятностей
случайного процесса
и функцию распределения вероятностей
случайного процесса ![]() , где
, где ![]() –
гауссовская случайная величина с параметрами
–
гауссовская случайная величина с параметрами ![]() и
и ![]() ,
, ![]() –
неслучайная величина.
–
неслучайная величина.
7. Найти ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() и функцию распределения вероятностей
случайного процесса
и функцию распределения вероятностей
случайного процесса ![]() , где
, где ![]() –
случайная величина, равномерно распределенная на интервале
–
случайная величина, равномерно распределенная на интервале ![]() ;
; ![]() –
неслучайная величина.
–
неслучайная величина.
8. Найти ![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() и
и ![]() случайного процесса
случайного процесса ![]() , где
, где ![]() –
гауссовская случайная величина с плотностью распределения вероятностей
–
гауссовская случайная величина с плотностью распределения вероятностей
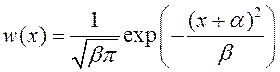 .
.
9. Случайный процесс ![]() , где
, где ![]() и
и ![]() – некоррелированные гауссовские случайные
величины с одинаковыми математическими ожиданиями и дисперсиями. Найти
– некоррелированные гауссовские случайные
величины с одинаковыми математическими ожиданиями и дисперсиями. Найти ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() и
и
![]() случайного процесса
случайного процесса ![]() .
.
10. Двумерная плотность распределения
вероятностей случайного процесса ![]() равна
равна
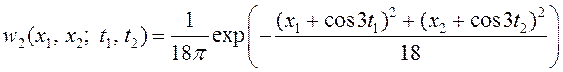 .
.
Найти
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() случайного процесса
случайного процесса ![]() .
.
11. Двумерная плотность распределения
вероятностей случайного процесса ![]() равна
равна
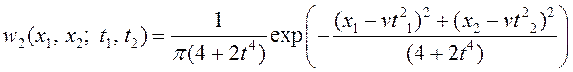 , где
, где
![]() – неслучайная величина. Найти
– неслучайная величина. Найти ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() случайного процесса
случайного процесса ![]() .
.
12. Ковариационная функция случайного
процесса ![]() равна
равна
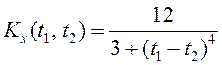 .
.
Найти ковариационную функцию и дисперсию процесса
![]() .
.
13. Найти ![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() случайного процесса
случайного процесса
![]() , где
, где ![]() –
случайная величина, равномерно распределенная на интервале
–
случайная величина, равномерно распределенная на интервале ![]() ;
; ![]() и
и ![]() – неслучайные величины.
– неслучайные величины.
14. Определить ковариационную функцию и дисперсию случайного процесса
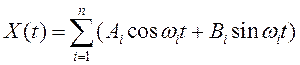 , где
, где ![]() и
и ![]() – взаимно некоррелированные случайные величины
с нулевыми математическими ожиданиями и одинаковыми дисперсиями.
– взаимно некоррелированные случайные величины
с нулевыми математическими ожиданиями и одинаковыми дисперсиями.
15. Доказать, что корреляционная функция
произведения ![]() взаимно независимых случайных процессов с
нулевыми математическими ожиданиями равна произведению их корреляционных
функций.
взаимно независимых случайных процессов с
нулевыми математическими ожиданиями равна произведению их корреляционных
функций.
16. Математическое ожидание и
ковариационная функция случайного процесса ![]() заданы
выражениями
заданы
выражениями
![]() и
и ![]() .
.
Найти ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() случайного процесса
случайного процесса ![]() .
.
17. Заданы два случайных процесса: ![]() и
и ![]() , где
, где ![]() и
и ![]() –
неслучайные величины;
–
неслучайные величины; ![]() и
и ![]() –
взаимно коррелированные случайные величины (
–
взаимно коррелированные случайные величины (![]() ) с нулевыми
математическими ожиданиями и одинаковыми дисперсиями. Найти взаимную
ковариационную функцию случайных процессов
) с нулевыми
математическими ожиданиями и одинаковыми дисперсиями. Найти взаимную
ковариационную функцию случайных процессов ![]() и
и ![]() .
.
18. Найти взаимную корреляционную и
взаимную ковариационную функции двух случайных процессов ![]() и
и ![]() , где
, где ![]() и
и ![]() –
взаимно некоррелированные случайные величины, равномерно распределенные на
интервалах
–
взаимно некоррелированные случайные величины, равномерно распределенные на
интервалах ![]() и
и ![]() .
.
19. Известны математические ожидания ![]() ,
, ![]() и
ковариационные функции
и
ковариационные функции ![]() и
и ![]() некоррелированных случайных процессов
некоррелированных случайных процессов ![]() и
и ![]() . Найти
моментные функции процесса
. Найти
моментные функции процесса ![]() .
.
20. Найти ![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() случайного процесса
случайного процесса ![]() , где
, где ![]() и
и ![]() –
взаимно некоррелированные случайные величины, распределенные по законам
–
взаимно некоррелированные случайные величины, распределенные по законам
![]() и
и ![]()
21. Какими из перечисленных ниже свойств всегда обладает ковариационная функция стационарного случайного процесса:
а) эта функция не отрицательная;
б) эта функция четная;
в) позволяет найти математическое ожидание;
г) позволяет найти дисперсию случайного процесса;
д) в нуле имеет максимальное значение.
22. Задан случайный процесс
![]() , где
, где ![]() –
случайная величина, равномерно распределенная на интервале
–
случайная величина, равномерно распределенная на интервале ![]() . Является ли
. Является ли ![]() стационарным
случайным процессом?
стационарным
случайным процессом?
23. Задан случайный процесс
![]() , где
, где ![]() – случайная величина, равномерно
распределенная на интервале
– случайная величина, равномерно
распределенная на интервале ![]() ;
; ![]() – стационарный случайный процесс. Является
ли
– стационарный случайный процесс. Является
ли ![]() стационарным случайным процессом?
стационарным случайным процессом?
24. Даны корреляционные функции эргодических случайных процессов, описываемые выражениями:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) 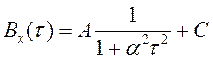 ;
;
д) ![]() ;
;
е) ![]() .
.
Найти дисперсии,
ковариационные функции, нормированные корреляционные функции, абсолютные
значения математических ожиданий и интервалы корреляции ![]() и
и
![]() этих процессов.
этих процессов.
25. Заданы случайные процессы
![]()
и
![]() , где
, где ![]() и
и
![]() – некоррелированные случайные величины,
равномерно распределенные на интервале
– некоррелированные случайные величины,
равномерно распределенные на интервале ![]() .
Доказать, что данные случайные процессы стационарно связаны.
.
Доказать, что данные случайные процессы стационарно связаны.
26. Задан случайный процесс
![]() , где
, где ![]() –
эргодический случайный процесс с корреляционной функцией
–
эргодический случайный процесс с корреляционной функцией ![]() . Является ли
. Является ли ![]() стационарным
случайным процессом? Найти дисперсию
стационарным
случайным процессом? Найти дисперсию ![]() и интервал корреляции
и интервал корреляции ![]() процесса
процесса ![]() , как
функции параметра
, как
функции параметра ![]() . При каких условиях дисперсия
процесса
. При каких условиях дисперсия
процесса ![]() больше дисперсии процесса
больше дисперсии процесса ![]() ?
?
27. Одномерная плотность распределения
вероятностей и корреляционная функция эргодического процесса ![]() заданы выражениями:
заданы выражениями:
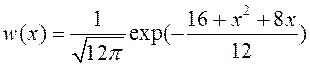 ,
,
![]() .
.
Найти параметры ![]() и
и ![]() .
.
28. Корреляционная функция эргодического
гауссовского случайного процесса ![]() равна
равна ![]() . Найти одномерную плотность распределения
вероятностей процесса
. Найти одномерную плотность распределения
вероятностей процесса ![]() , если математическое ожидание
меньше нуля.
, если математическое ожидание
меньше нуля.
29. Случайный процесс ![]() равен сумме двух статистически независимых
эргодических случайных процессов
равен сумме двух статистически независимых
эргодических случайных процессов ![]() и
и ![]() с отрицательными математическими
ожиданиями и корреляционными функциями, заданными выражениями:
с отрицательными математическими
ожиданиями и корреляционными функциями, заданными выражениями:
![]()
и
![]() .
.
Определить математическое
ожидание и дисперсию процесса ![]() .
.
30. Случайный процесс ![]() равен произведению двух взаимно
некоррелированных эргодических случайных процессов
равен произведению двух взаимно
некоррелированных эргодических случайных процессов ![]() и
и ![]() с корреляционными функциями, заданными выражениями:
с корреляционными функциями, заданными выражениями:
![]()
и
![]() .
.
Определить математическое
ожидание, дисперсию и корреляционную функцию процесса ![]() .
.
31. Найти спектральную плотность мощности случайного процесса
![]() , где
, где ![]() и
и
![]() – некоррелированные случайные величины с
нулевым математическим ожиданием и одинаковой дисперсией.
– некоррелированные случайные величины с
нулевым математическим ожиданием и одинаковой дисперсией.
32. Найти спектральную плотность мощности
случайного процесса ![]() , если спектральная плотность
мощности стационарного процесса
, если спектральная плотность
мощности стационарного процесса ![]() равна
равна
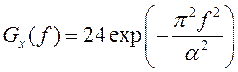 .
.
33. Могут ли следующие функции быть корреляционными функциями
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.