Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 9

Направление действия угловой скорости шатуна 4  указывает вектор ускорения , перенесенный с плана скоростей в точку Dна схеме механизма. Точка С условно делается  неподвижной. При этом разрывается связь между коромыслом 3, ползуном 5. В этом случае точка Dсовместно с шатуном 4 под действием вектора   получает, возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки С. Полученное  направление вращательного движения шатуна 4 будет являться направлением действия угловой ускорения данного звена.

Угловое ускорение коромысла 3 найдем по формуле:

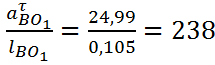= рад/c

Направление действия угловой скорости коромысла 3  указывает вектор скорости , перенесенный с плана скоростей в точку В на схеме механизма. Точка О₁ является  неподвижной. При этом разрывается связь между коромыслом 3 и шатуном 2. В этом случае точка В совместно с коромыслом 3 под действием вектора   получает возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки О₁. Полученное  направление вращательного движения коромысла 3 будет являться направлением действия угловой скорости данного звена.

Ползун 5 совершает только поступательное движение, следовательно, угловое ускорение этого звена равно нулю, т. е. = 0 рад/с.

8.  Кинетостатический (силовой) анализ сложного плоского рычажного механизма.

8.1  Составление расчетной схемы: определение величин, линий и направлений действия сил тяжести, сил и моментов пар сил инерции.

Для проведения силового анализа воспользуемся кинетостатическим методом, основанным на принципе Даламбера (в число заданных сил при расчёте входят силы инерции), при этом определим реакции связей кинематических пар и уравновешивающую силу (уравновешивающий момент).

Возьмем четвёртое положение механизма и построим его в масштабном коэффициенте длин μ_l;

Рассчитаем силы, действующие на звенья.

Сила тяжести G_i равна:

G_i=m_i ∙g,                                                (4.1)

G_i  - сила тяжести i-го звена, Н;

m_i - масса i-го звена, кг;

g– ускорение свободного падения, 9,81 м/с² .

Масса звена  определяем по формуле:

m_i=k_i ∙ l_i                                                (4.2)

m_i – масса i-го звена, кг;

k_i - удельная масса i-го звена, кг/м;

l_i – длина i-го звена, м.

Удельные массы равны:

для кривошипов k=(8…10), кг/м.

для шатунов k=(12…20), кг/м.

для коромысла k=(20…40), кг/м.

Масса ползуна рассчитывается по формуле:

m_{ползуна}= (0,5…0,7) ∙ m_шатуна                              (4.3)

m_{ползуна} – масса ползуна, кг;

m_шатуна – масса шатуна, к которому прикреплен ползун, кг.

По формулам (4.2) и (4.3) определим массы звеньев:

m₁ = k_{кривошип} ∙ l_AO = 9∙0,058 = 0,522кг,

m₂ = k_шатун ∙ (l_AB+l_BC) = 15 ∙ (0,233+0,035) = 4,02 кг,

m₃= k_{коромысла} ∙  =30 ∙ 0,105 = 3,15 кг,

m₄ = k_шатун ∙ l_DC=15 ∙ 0,325 = 4,875 кг,

m₅ = (0,5…0,7) ∙ m_шатуна =0,6 ∙ 4,875 = 2,925 кг,

По формуле (4.1) определим силы тяжести звеньев:

G₁= 0,522 ∙ 9,81 = 5,121 H

G₂= 4,02 ∙ 9,81 = 39,44 H

G₃= 3,15 ∙ 9,81 = 30,9 H

G₄= 4,875 ∙ 9,81 = 47,82 H

G₅= 2,925 ∙ 9,81 = 14,26 H

Вектора сил тяжести звеньев механизма направлены вертикально вниз. Сила тяжести первого звена приложена в точке  О, силы тяжести второго, третьего и четвёртого звеньев приложены в точках , и , а сила тяжести пятого звеньев приложена в точке D.

Определим силы инерции звеньев.

Вектор силы инерции   может быть определен по формуле:

 (4.4)

 – вектор силы инерции i-го звена;

 – масса i-го звена, кг;

 – вектор полного ускорения центра масс i-го звена.

Момент пары сил инерции направлен противоположно угловому ускорению  и может быть определён по формуле:

                                              (4.5)

– момент пары сил инерции i-го звена, Н·м;

– момент инерции i-го звена относительно оси, проходящей через центр масс s_i и перпендикулярной к плоскости движения звена, кг ∙ м²;