Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 2

Из анализа данных таблицы 2 следует, что исследуемый механизм состоит из семи кинематических пар: пяти пар пятого класса, одной пары четвертого класса и одной пары третьего класса. Следовательно, их коэффициенты равны: p₅=5,  p₄=1, p₃=1,  p₂=0,  p₁=0.

Из анализа таблиц 1 и 2 следует, что данный механизм образует одну простую незамкнутую кинематическую цепь (т.к каждое звено которой входит в состав не более двух кинематических пар, т. е. содержит только одно или два вершины звена и в которой хотя бы одно звено имеет свободный элемент, не взаимодействующий с другими звеньями и не образующий с ними кинематических пар, в данном случае это схват 7) и содержит в своей структуре один элемент стойки, представленный звеном 0.

Полученные значения подставляем в формулу (1.0), получим:

W=6∙7-5∙5-4∙1-3∙1-2∙0-1∙0=42-25-4-3-0-0=10

Результат означает, что для однозначного определения взаимного расположения звеньев данного механизма трехмерного пространства при не замкнутой кинематической цепи, необходимо 10 обобщенных координат.

Определение маневренности:

Для определения маневренности механизма необходимо, что бы кинематическая цепь была замкнутой. Для этого схват изображаем как неподвижное звено. Кинематическая цепь становиться замкнутой и поэтому число подвижных звеньев уменьшается на (n-1), тогда n=6.

На (рис.2) изображена структурная схема замкнутого пространственного механизма.

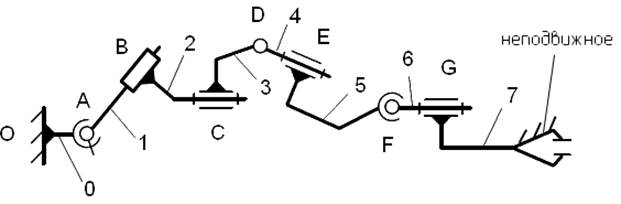Рис.2

Рис. 2

m=6∙n - 5∙p₅ - 4∙p₄- 3 p₃- 2 p₂- p₁                              (1.1)

m– Маневренность манипулятора.

Подставив известные данные в формулу (1.1), получим:

m=6∙6 - 5∙5 - 4∙1 - 3∙1 - 2∙0 - 1∙0=4

Результат означает, что для однозначного описание взаимного расположения звеньев данного механизма в трехмерном пространстве при замкнутой кинематической цепи, достаточно 4-х обобщенные координат.

Проверка:

m=W-6=10-6=4

m ≥ 4

Условие проверки сходиться, так как значения маневренности должны быть m ≥ 1

Вывод: из рассмотренных ситуаций следует, что обеспечение работоспособности манипулятора возможно только при выполнении следующего условия:  m ≥ 4

5.2  Определения подвижности (степени подвижности) и анализ состава структуры сложного плоского рычажного механизма.

Определения подвижности:

На рисунке 3 изображена схема сложного плоского рычажного механизма:

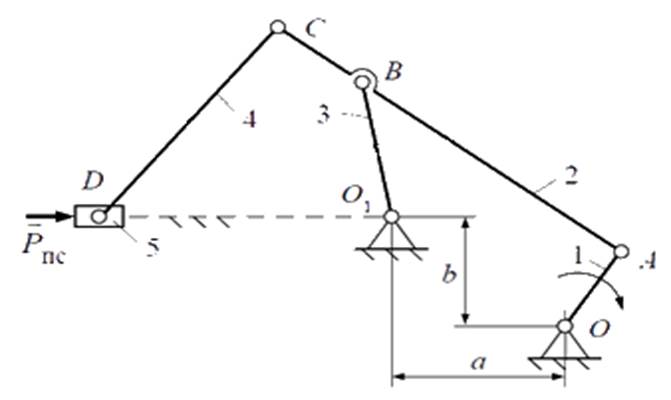Рис. 3

Для определения подвижности сложного плоского рычажного механизма воспользуемся структурной формулой Чебышева:

W=3∙n-2p₅-p₄         (1.2)

Для определения величины коэффициента n проанализируем структурную схему механизма (рис.3), результат представим в виде таблицы:

Таблица 3.

Проанализировав структурную схему механизма, из таблицы 3 видно, что механизм состоит из шести звеньев: 1-кривошипа, 2-шатуна, 3-коромысла, 4-шатуна, 5-ползуна, 0-стойки. При этом звенья 1-5 являются подвижными звеньями, а стойка 0-неподвижным звеном, она представлена в составе структурной схемы направляющей ползуна 5 и двумя шарнирно-неподвижными опорами О и О₁. Следовательно, n=5 .

Для определения значений коэффициентов p4 и p5 найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследования заносим в таблицу 4:

Таблица 4.