Машиностроение \ Теория машин и механизмов

Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 6

Подставляем заданные значения в формулу(3.1) получим:

ω1=

VA=VAO=ω1∙lOA=29,32∙0,058=1,7м/с

Масштабный коэффициент плана скоростей μv равен:

μv =                                            (3.2)

VA − модуль скорости т.A;

|pa| − произвольно выбранный отрезок, изображающий на плане скоростей вектор скорости т. A.

Примем , тогда по выражению (3.2) получим:

μv=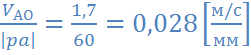

Из произвольно выбранной точки  (полюс скоростей) откладываем перпендикуляр к кривошипу 1, на котором будет находиться вектор скорости т.А. Затем от полюса откладываем отрезок равный |pa|=60мм и получаем точку а. Вектор A перпендикулярен кривошипу ОА и направлен в сторону его вращения.

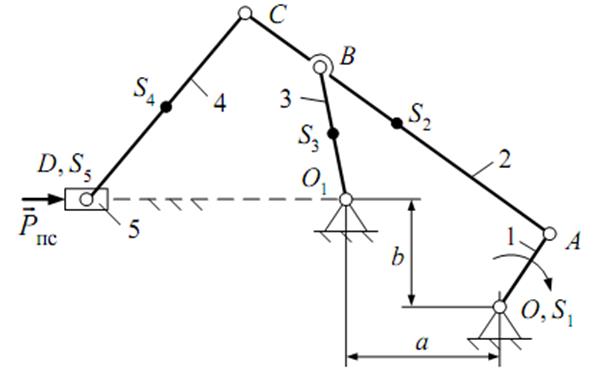
Рассмотрим точку В:

Вектор скорости т.B, принадлежащей шатуну 2, представляет собой геометрическую сумму вектора скорости т.А и вектора скорости относительного вращательного движения т.B вокруг т.А:

B=A+                                              (3.3)

В то же время т.B принадлежит и коромыслу 3. Коромысло 3 совершает только вращательное движение вокруг т.О1 принадлежащей стойке и траекторией движения является кривая 2-го порядка, т. е окружность.

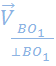B=A+(3.4)

Из точки a проводим линию, перпендикулярную шатуну АВ, а из полюса прямую, перпендикулярную прямой BO1. На пересечении этих двух перпендикуляров мы получим точку bи откладываем вектора скоростей  и .

Рассмотрим точку С:

Вектор скорости точки С, найдем при помощи теоремы подобия:

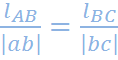                                                   (3.5)

Из формулы (3.5) выразим длину отрезка  отложим его из точки b, мы получим точку С и вектор скорости .

Рассмотрим точку D:

Вектор скорости т.D, принадлежащей шатуну 4, представляет собой геометрическую сумму вектора скорости т.Cи вектора скорости относительного вращательного движения т.Dвокруг т.C:

D=C+(3.6)

В то же время т.Dпринадлежит и ползуну 5. Ползун 5 совершает только прямолинейные поступательное движение вдоль направляющей (прямая DO1), следовательно, линия действия вектора скорости т.Dпроходит параллельно прямой DO1:

D||DO1(3.7)

Из точки c проводим линию, перпендикулярную шатуну CD, а из полюса прямую, параллельную прямой DO1. На пересечении получим точку d и получим векторы скоростей D и CD.

Определим значения скоростей характерных точек.

Замерив на плане скоростей для четвертого положения длины отрезков |pb|, |ab|, |pd|,|cd|, |bc| и  получим:

Используя найденные величины отрезков, определим модули соответствующих скоростей для четвертого положения механизма.

=|pb| ∙ μυ = 51,27 ∙ 0,028 = 1,44 м/с

VBA=|ab| ∙ μυ = 16,07 ∙ 0,028 = 0,45 м/с

VCB=|bc| ∙ μυ = 2,41 ∙ 0,028 = 0,07 м/с

VDC=|cd| ∙ μυ = 50,45 ∙ 0,028 = 1,41 м/с

VD=|pd| ∙ μυ = 4,46 ∙ 0,028 = 0,13 м/с

VC=|pc| ∙ μυ = 50,28 ∙ 0,028 = 1,41 м/с

Таблица 5.

Номер положения механизма

Скорости точек,

Угловые скорости звеньев,

1

1,7

1,09

0,92

1,04

0,14

0,3

0,9

29,32

3,95

10,38

2,77

2

1,7

1,58

0,41

1,58

0,06

0,35

1,45

29,32

1,76

15,05

4,46

3

1,7

1,68

0,1

1,68

0

0,09

1,66

29,32

0,43

16

5,11

4

1,7

1,44

0,45

1,41

0,07

0,12

1,41

29,32

1,93

13,71

4,34

5

1,7

0,81

1,09

0,74

0,15

0,07

0,74

29,32

4,68

5,4

2,28

6

1,7

0

1,68

0,25

0,25

0,25

0

29,32

7,21

0

0

7

1,7

0,67

1,77

0,8

0,27

0,45

0,68

29,32

7,6

6,38

2,09

8

1,7

1,19

1,26

1,22

0,19

0,39

1,18

29,32

5,41

11,3

3,63

9

1,7

1,64

0,14

1,64

0,02

0,03

1,64

29,32

0,6

15,62

5,05

10

1,7

1,86

1,31

1,96

0,2

0,76

1,69

29,32

5,62

17,71

5,2

11

1,7

1,28

2,1

1,49

0,32

0,87

0,97

29,32

9,01

12,19

2,98

12,0

1,7

0,04

1,61

1,91

0,24

0,25

0,9

29,32

6,91

0,38

2,77

13

1,7

0,04

1,61

1,91

0,24

0,25

0,9

29,32

6,91

0,38

2,77
Скачать файл