![]() – угловое ускорение i-го звена, рад/с2.
– угловое ускорение i-го звена, рад/с2.
Момент инерции шатуна 2 определяется по формуле:
![]() (4.6)
(4.6)
Момент инерции шатуна 4 определяется по формуле:
![]() (4.7)
(4.7)
Момент инерции коромысла 3 определяется по формуле:
![]() (4.8)
(4.8)
Рассчитаем силы инерции по формуле (4.4):
![]() H
H
![]() H
H
![]() H
H
![]() H
H
![]() H
H
Вектора сил
инерции
![]() ,
, ![]() и
и ![]() лежат на прямых, параллельных, соответственно,
линиям действия векторов ускорений центров масс
лежат на прямых, параллельных, соответственно,
линиям действия векторов ускорений центров масс ![]() ,
, ![]() и
и ![]() , а направление действия этих векторов
противоположно направлению действия векторов ускорений центров масс этих
звеньев.
, а направление действия этих векторов
противоположно направлению действия векторов ускорений центров масс этих
звеньев.
Рассчитаем моменты инерции шатунов по формуле (4.6), (4,7) и (4.8):
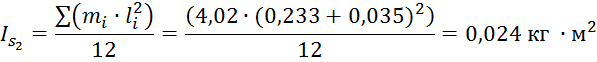
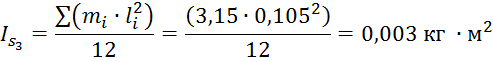
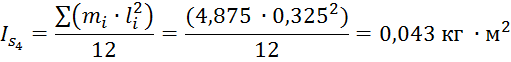
Рассчитаем моменты пар сил инерции для второго, третьего и четвертого звеньев по формуле (4.5):
![]()
![]()
![]()
Момент пар сил инерции для 1-го звена равен 0 т. к. ε1=0 рад/с2. Для 5-го так же момент пар сил будет равен 0, т.к. ползун 5 совершает только поступательное движение.
Направления действия моментов пар сил инерции противоположно направленно действию углового ускорения.
Заменим моменты инерции звеньев парами сил по формуле:
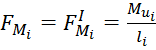 (4.9)
(4.9)
![]() и
и ![]() - пара сил, действующая на i – ое звено;
- пара сил, действующая на i – ое звено;
![]() – момент инерции i – го звена;
– момент инерции i – го звена;
![]() - длина i – го звена.
- длина i – го звена.
Рассчитаем значение пары сил для второго, третьего и четвертого звена:
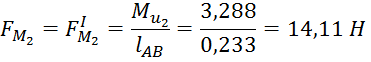
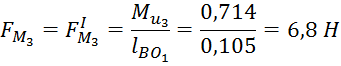
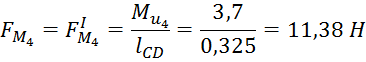
Покажем на чертеже моменты пар сил инерции шатунов и укажем направление силы полезного сопротивления.
8.2 Определение уравновешивающей силы с помощью теоремы И. Е. Жуковского.
Для применения теоремы Жуковского
построим повёрнутый план скоростей. Перенесём все силовые факторы с расчетной
модели в соответствующие точки повёрнутого плана скоростей. Положение точек ![]() ,
, ![]() и
и ![]() определим используя теорему подобия.
определим используя теорему подобия.
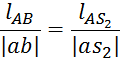
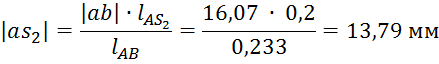
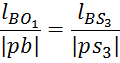
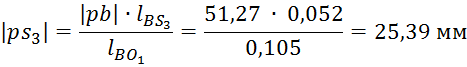
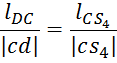
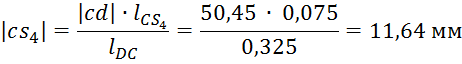
Составим уравнение моментов относительно полюса плана:
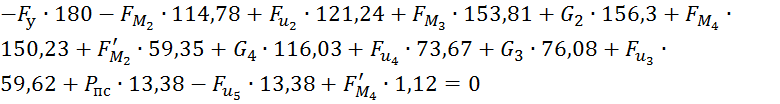
Определим значение силового управляющего воздействия:
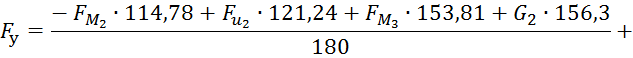
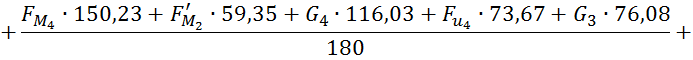
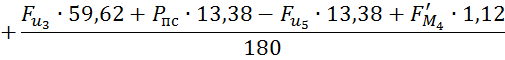
Из данного выражения следует, что ![]()
Определим значение уравновешивающего момента по формуле :
![]() (4.10)
(4.10)
![]()
8.3 Метод кинетостатики для одного положения кривошипа; силовой анализ структуры групп и первичного механизма (приведение сил). Определение величины уравновешивающей силы и уравновешивающего момента пары сил.
Для применения кинетостатического метода вычертим структурные группы звеньев и первичный механизм в заданном масштабном коэффициенте длин. Приложим к звеньям структурных групп и первичного механизма вектора сил. Установим для структурных групп и первичного механизма состояние силового равновесия, приложив к соответствующим характерным точкам реакции связей.
Структурной группы звеньев 4 – 5
Рассмотрим структурную группу звеньев 4-5. Запишем уравнение кинетостатического равновесия:
![]() (4.11)
(4.11)
В уравнении (4.11), содержится три
неизвестных силовых фактора (![]() ), т.к. решение в векторном виде на плоскости
возможно только для двух неизвестных сил, то система является один раз
статически неопределимой.
), т.к. решение в векторном виде на плоскости
возможно только для двух неизвестных сил, то система является один раз
статически неопределимой.
Раскроем статическую неопределимость, составив уравнение моментов относительно т. D.
![]() (4.12)
(4.12)
![]()
Откуда
выразим ![]() :
:
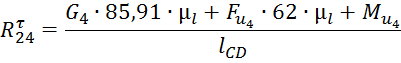
Подставляем численные значения и получаем:
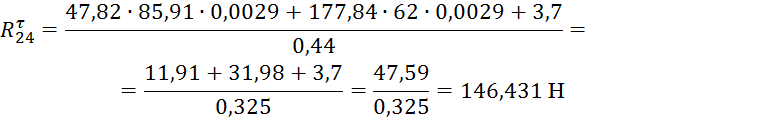
Таким образом, в
уравнении осталось 2-е неизвестных силы (![]() ), их можно найти, составлением векторного силового
многоугольника.
), их можно найти, составлением векторного силового
многоугольника.
Для его построения выберем масштабный коэффициент сил:
![]() (4.13)
(4.13)
![]() – истинное значение известной максимальной силы,
входящей в уравнение;
– истинное значение известной максимальной силы,
входящей в уравнение;
![]() – отрезок, изображающий длину этой силы на плане скоростей,
принимаем
– отрезок, изображающий длину этой силы на плане скоростей,
принимаем ![]() мм;
мм;
Определяем масштабный коэффициент сил по формуле (4.13) получаем:
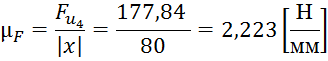
Далее производим расчет длин векторов для плана сил:
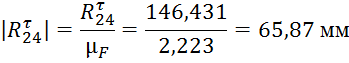
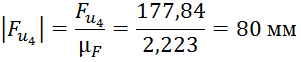
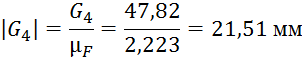
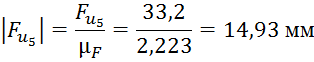
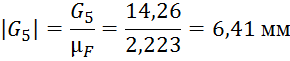
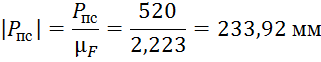
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.