Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 11

Из произвольной точки строим вектор , затем из конца этого вектора  строим вектор  и так далее по уравнению. Завершаем многоугольник сил, проводя из начала вектора , прямую параллельную DC, а из конца вектора  прямую, перпендикулярную OD.  Точка пересечения позволяет построить силы ,  и  на плане сил и определить их истинное значение.

 Н

Н

Н

Структурной группы звеньев 2-3.

Рассмотрим структурную группу звеньев 2-3. Запишем уравнение кинетостатического равновесия:

           (4.14)

Сила реакции со стороны четвёртого звена на второе:

В уравнении (4.14), содержится четыре неизвестных силовых фактора (), т.к. решение в векторном виде на плоскости возможно только для двух неизвестных сил, то система является дважды статически неопределимой.

Раскроем статическую неопределимость, составив уравнение моментов относительно т. B.

                                                   (4.15)

Относительно шатуна 2:

Откуда выразим :

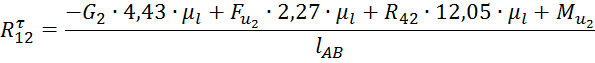
Подставляем численные значения и получаем:

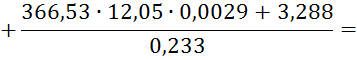
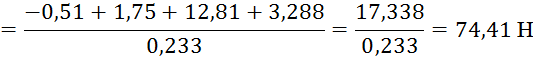
Относительно коромысла 3:

Откуда выразим :

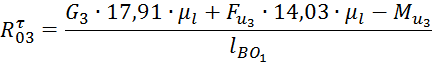
Подставляем численные значения и получаем:

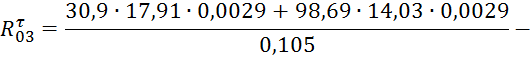
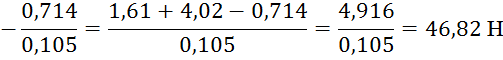
Таким образом, в уравнении осталось 2-е неизвестных силы (), их можно найти, составлением векторного силового многоугольника.

Для его построения выберем масштабный коэффициент сил:

                                                 (4.13)

 – истинное значение известной максимальной силы, входящей в уравнение;

 – отрезок, изображающий длину этой силы на плане скоростей, принимаем  мм;

Определяем масштабный коэффициент сил по формуле (4.13) получаем:

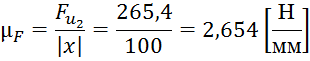
Далее производим расчет длин векторов для плана сил:

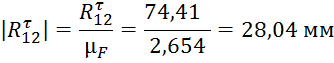
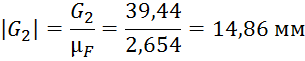
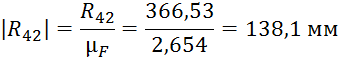
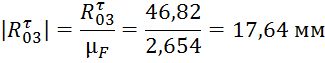
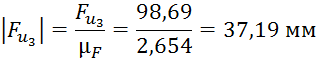
Из произвольной точки строим вектор , затем из конца этого вектора  строим вектор  и так далее по уравнению. Завершаем многоугольник сил, проводя из начала вектора , прямую параллельную AB, а из конца вектора  прямую, параллельную O₁B.  Точка пересечения позволяет построить силы  на плане сил и определить их истинное значение.

  Н

Н

 Н

Н

Составим уравнение равновесия для первичного механизма.

В представленном уравнении содержится 3-и неизвестных силовых фактора (), так как решение в векторном виде на плоскости возможно только для двух неизвестных сил система является один раз статически неопределимой.

Раскроем статическую неопределимость, составив уравнение моментов относительно точки А.

                                                  (4.15)

Откуда выразим :

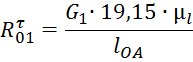
Подставляем численные значения и получаем:

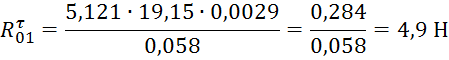
Таким образом, в уравнении осталось 2-е неизвестных силы (), их можно найти, составлением векторного силового многоугольника.

Для его построения выберем масштабный коэффициент сил:

                                                 (4.16)

 – истинное значение известной максимальной силы, входящей в уравнение;

 – отрезок, изображающий длину этой силы на плане скоростей, принимаем  мм;

Определяем масштабный коэффициент сил по формуле (4.16) получаем:

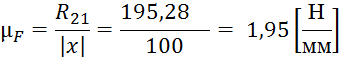
Далее производим расчет длин векторов для плана сил:

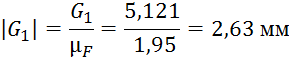
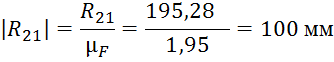
Из произвольной точки строим вектор , затем из конца этого вектора  строим вектор  и так далее по уравнению. Завершаем многоугольник сил, проводя из начала вектора , прямую параллельную OA, а из конца вектора  прямую, перпендикулярную OA.  Точка пересечения позволяет построить силы ,  и  на плане сил и определить их истинное значение.

Определим значение уравновешивающего момента по формуле (4.17):

                                               (4.17)

Подставляем численные значения и получаем:

  Н∙м.

8.4   Определение погрешности выполненного анализа.

Определим погрешность результатов по формуле:

                               

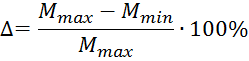
 – максимальное значение уравновешивающего момента, полученного в результате двух расчетов, метода кинетостатически и метода Жуковского.

 – минимальное значение уравновешивающего момента, полученного в результате двух расчетов, метода кинетостатически и метода Жуковского.